本文書は,日本における RDF および RDFS の普及を目的に, http://www.w3.org/TR/2004/REC-rdf-mt-20040210/を日本語訳したものである.
いかなる組織,個人でも,原文およびW3Cの Copyright に従う限りにおいて,本訳をどのように使用してもよいが,それによって生ずる結果について,
翻訳者は一切の責任を負わない.
注意深く訳したつもりであるが,誤りがあり得ることは否定できない.誤りの指摘を大いに歓迎する.コメントその他は翻訳者まで送られたい.
小出 誠二 2012年 6月1日改訂
小出 誠二 2008年12月1日初版
アブストラクト
本文書は Resource Description Framework (RDF) と RDF Schema (RDFS)
に対する精密な意味論と,それに一致する推論ルールの完全なシステムの仕様である.
目次
0. はじめに
0.1 形式意味論の仕様明細:範囲と限界
0.2 グラフ構文論
0.3 グラフ定義
1. 解釈
1.1 技術ノート (情報提供)
1.2 URI 参照, リソース そして リテラル
1.3 解釈
1.4 基底グラフの表示的意味
1.5 存在変数としてのブランクノード
2. RDF グラフ間の単純伴意
2.1 語彙の解釈と語彙の伴意
3. RDF 語彙の解釈行為
3.1 RDF 解釈
3.2 RDF 伴意
3.3 具体化, コンテナ, コレクション そして rdf:value
3.3.1 具体化 (Reification)
3.3.2 RDF コンテナ
3.3.3 RDF コレクション
3.3.4 rdf:value
4. RDFS 語彙の解釈
4.1 RDFS 解釈
4.2 外延的意味論の条件 (情報提供)
4.3 rdfs:Literal に関するノート
4.4 RDFS 伴意
5. データタイプの解釈
5.1 データタイプでタイプ付けされた解釈
5.2 D-伴意
6. 意味論的外延の単調性
7. 伴意ルール (情報提供)
7.1 単純伴意ルール
7.2 RDF 伴意ルール
7.3 RDFS 伴意ルール
7.3.1 外延の伴意ルール
7.4 データタイプの伴意ルール
付録 A. レンマの証明 (情報提供)
付録 B. 用語集 (情報提供)
付録 C. 謝辞
参考資料
付録 D. 変更ログ (情報提供)
RDF は WWW 上のアクセスや使用のために,形式的で厳密な語彙,特にRDFS [RDF-VOCABULARY]
において仕様記述された語彙を用いて,命題を表現するために用いられることが意図された
宣言型言語 (assertional language) であり,同様な目的のより進んだ宣言型言語のための基盤を提供することが意図されている.
その全体の設計目標は,特定の処理モデルに合わせるのではなく,どんなトピックについての命題も汎用的に正確に表現することにある.
より詳細な議論はRDF 概念[RDF-CONCEPTS] を
参照されたい.
広義において RDF あるいは RDFS における表明の「意味」(meaning) が何であるかと考えることは,
厳密には,社会的慣習,自然言語によるコメント,あるいは他の内容を伝える文書も含め,多くの要因に依存し得る.
こういった意味の多くは機械処理によるアクセスは不可能であり,本文書において記述される
形式意味論が
この広義の意味で '意味' の完全な分析を提供することは意図されていないということを
単に強調したいがために,ここでそれについて述べただけである.それは大きな研究トピックであろう.ここで与えられる意味論は,
意味の形式的な考え方に制限されており,
意味についてのその他のすべての説明に共通な部分として特徴づけられるようなものであり,
機械的推論ルールで処理することができるものである.
本文書では,形式言語の意味論を特定するために,
モデル理論 (model theory) と呼ばれる基礎技術が用いられる.
モデル理論に不慣れな読者は付録 B の 用語集 が助けになるだろう.
本テキストを通じて,使用される用語は技術的な語義について用語集にある定義にリンクづけされている.
モデル理論では,言語はある「世界 (world) 」について言及し,
その言語におけるすべての表現に対してある適切な意味を割り当てるために,世界が充足 (satisfy) しなければならない最小条件を記述するものと仮定される.
ある特定の世界は解釈 (interpretation) と呼ばれ,
そのため モデル理論はより正しくは「解釈理論」と呼んでもいいかも知れない.
この考え方は,解釈の実際の性質や本質的な構造についてできるだけ少ない仮定を立てて,それによってできるだけ汎用性を維持するといった,
どんな解釈でも備えなければならない性質について,抽象的な,数学的な説明手段を提供する.
形式意味論の主要な効用は,その言語によって記述されている事物の性質について深い分析を提供したり,何か特定の処理モデルを提供することではなく,
むしろどんなときに推論プロセスが正当 (valid) であるか,すなわち真実を保持するか,
を決定する技術的手段を提供することにある.これは意味について大域的な整合性のある考え方を保持する一方で,実装には最大の自由を提供する.
モデル理論は形而上学的に,
かつオントロジー的に中立であろうとする.
それは典型的には単純に集合理論の言い方で述べられる,なぜならばそれが数学における標準言語だからである.
例えば,この意味論では名前は「ユニバース (universe) 」と呼ばれるある集合 IR 中の事物を表示する (denote) .
しかしながら,ここでの集合論的言語の使用は,ユニバース中の事物が本来集合論的であるということを暗に意味するというわけではない.
モデル理論は通常伴意 (entailment) という考え方(後述)を通じて実装にたいていの場合関連する.
それは正当な推論ルールを定義することを可能にするものである.
意味論を明記するもう一つの方法は,すでに関連付けられたモデル理論をそのまま使って,
RDF から形式論理への変換を与えることである. この「公理的意味論」のアプローチはターゲットである論理言語の様々なバージョン,
[Conen&Klapsing]
[Marchiori&Saarela]
[McGuinness&al],で提案され用いられてきた.
RDF と RDFS のためのそのような変換は Lbase 仕様[LBASE] でも与えられている.
公理的意味論のスタイルは機械処理に優れていてより可読性が高いかも知れないが,どんな公理的意味論でも,
本文書で述べられるモデル理論の意味論に適合しないという場合には,モデル理論が規範となるべきである.
RDF における意味には意味論では無視されるいくつかの点がある.特に,URI 参照は単純な名前として扱われ,
特定の URI 形式 [RFC 2396] でコード化される意味は無視されるし,時間変化の分析や URI 参照の変更も考慮されていない.
例えば「この文書」といった,URI 参照のインデックス的使用に関するどんな分析もされていない.
RDF と RDFS 語彙の一部では形式的意味が与えられていないし,時には,とりわけ具体化 (reification) とコンテナの語彙では,期待されるほどの意味は与えられていない.
これらの場合には本文中で注記され,その制限事項がより詳細に考察されている.
RDF は宣言的論理であり,そこでは各トリプルが単純な命題を表現する.
これはかなり厳密な単調増加の原則を言語に強いるので,閉世界仮説 (closed-world assumptions) ,
局所デフォールト選択 (local default preference) , そしていくつかの共通に用いられる 非単調の構成を表現できない.
DAML+OIL [DAML]
やOWL [OWL]
のようなより表現力の高い言語の基礎としての使用も含め,RDF
の特定の使用ではここで述べられるものに加えてさらに意味論的諸条件が重ね合わされてよく,そのような追加の意味論的諸条件は特定の RDF
語彙中の用語の意味に重ね合わすこともできる.
そのような追加の意味論的諸条件の重ね合わせにより得られる RDF の拡張ないし方言は RDF の意味論的拡張 (semantic extensions)
として言及される. RDF の意味論的拡張は,本勧告中では [RFC
2119] のキーワード,しなければならない ,してはならない,するべきである ,してもよい,で制限される. RDF の意味論的拡張は本文書の 1.3 節,1.4 節,1.5 節に記述される単純解釈の意味論的諸条件と,
3.1 節に記述の RDF 解釈の諸条件に適合しなければならない.
意味論的拡張における伴意のいかなる名前も語彙伴意の用語を用いて
指示されるべきである.
RDF の意味論的拡張に重ねあわされた意味論的諸条件は,本文書の規範的部分に記述されているモデル理論的意味論に正しく (valid) したがう語彙伴意の考え方を
定義しなければならない.ただし,
もしその意味論的拡張が構文論的に制限されたRDF グラフの部分集合で定義される場合には,
その意味論的諸条件はその部分集合に適用されるだけでよい.そのような構文論的に制限された意味論的拡張の明細は,
拡張された意味論的諸条件が適応されるところのその RDF グラフを曖昧さ無くソフトウェアが区別するに十分な構文論的な条件の明細を
含んでいなければならない.
そのような構文論的に制限された意味論的拡張に基づくアプリケーションは,
要求された構文論的制限に適合しないRDF グラフ を文法エラー (syntax error)
として扱うことをしてもよい.
RDF の意味論的拡張の一例は RDF Schema [RDF-VOCABULARY],
略して RDFS ,であり,その意味論は本文書の後半で定義される.RDF Schema はいかなる構文論的制限も追加しない.
どんな意味論でも構文論と組み合わされなければならない.ここでの意味論は RDF 概念と抽象構文の文書 [RDF-CONCEPTS]
に述べられている RDF 抽象構文への写像として定義される.
本文書ではそこで定義された以下の用語を用いる.
すなわち,URI 参照,
リテラル,
プレーンリテラル,
型付きリテラル,
XMLリテラル,
XML値,
ノード,
ブランクノード,
トリプル
そしてRDF グラフ である.
本文書を通じて,用語として「文字列 (character string もしくは string) 」を Unicode 文字のシーケンスを参照するために使い,
「言語タグ (langauge tag) 」を RFC 3066 の意味で使う ([RDF-CONCEPTS]
中の 6.5 節を参照のこと).
RDF グラフ中の文字列は Normal Form C であるべきであることに注意されたい.
本文書ではRDF
グラフを記述するために,RDF テストケース文書 [RDF-TESTS]
に述べられた N-トリプル構文を用いる.
この記法ではグラフのトリプル中のブランクノードを指定するのにノード指定子 (nodeID) を用いる.
「_:xxx」というように書かれるノード指定子は表面上の構文におけるブランクノードを同定するために用いられるが,
この表現はグラフノードを同定するラベルと考えられるべきではなく,名前でもなく,実際のグラフにおいて起こるものでもない.
特に,ノード指定子の名前だけが違うような二つの N-トリプル文書 で記述されるRDF グラフは,
等価とみなされる.
この改名の約束事は文書全体にのみ適応されるものと理解されるべきである.
もしある文書の一部だけにおいてノード指定子を改名すれば,結果として異なる RDF グラフを生じさせることになるかも知れない.
N-トリプル構文論では URI 参照はかぎ括弧 (angle bracket)
で括られた完全な形式で与えられる必要があるが,ここでは簡潔さのために,説明の例を提示するのに架空の URI スキーム「ex:」を用いる.
N-トリプル構文論の正規表現により本当に近い見栄えを得るためには,これを「http://www.example.org/rdf/mt/artificial-example/」
というようなもので置き換えるように思ってほしい.QName の接頭辞 (prefix) ,rdf:,rdfs: そして xsd:
は次のように定義されている.
Prefix rdf: 名前空間 URI: http://www.w3.org/1999/02/22-rdf-syntax-ns#
Prefix rdfs: 名前空間 URI: http://www.w3.org/2000/01/rdf-schema#
Prefix xsd: 名前空間 URI: http://www.w3.org/2001/XMLSchema#
QName 構文は正式な N-トリプル構文ではないが,簡潔さと可読性のために,便宜的にかぎ括弧で囲まれない QName でかぎ括弧で囲まれた相当する URI 参照を示す.
例えば,トリプル
<ex:a> rdf:type rdfs:Class .
は N-トリプル構文での次の省略形として読まれるべきである.
<ex:a> <http://www.w3.org/1999/02/22-rdf-syntax-ns#type> <http://www.w3.org/2000/01/rdf-schema#Class> .
一般的な意味論的諸条件を述べるとき,コロンなしの単一の文字や文字シーケンスは任意の名前,ブランクノード,文字列などを示す.
その正確な意味は文脈で明示されるだろう.
RDF グラフ
あるいは単にグラフ は,RDF トリプルの集合である.
RDF グラフの部分グラフ (subgraph)
はそのグラフのトリプルの部分集合である.一つのトリプルはそれを含むひとつの集合と同定されるので,
あるグラフ中の各トリプルは一つの部分グラフと考えられる.真 (proper) 部分グラフはそのグラフのトリプルの真部分集合である.
基底 (ground) RDF グラフはブランクノードのないグラフである.
名前 (name) は URI 参照またはリテラルである.
これらのものはある解釈によってある意味が割り当てられることが必要な表現である.
型付きリテラルは二つの名前すなわちリテラルと,その内部の型 URI 参照,から構成される
名前の集合は語彙 として言及される.
あるグラフの 語彙はそのグラフ中のどれかのトリプルのサブジェクト,プレディケイトあるいはオブジェクトとして現れる名前の集合である.
型付きリテラルの内部にしか現れない URI 参照はそのグラフの語彙とする必要はないことに注意されたい.
あるブランクノード集合からリテラル,ブランクノードそして URI 参照のある集合への写像 M を考えよう.
そのとき,あるグラフ G 中のブランクノード N のすべてあるいは一部を写像 M(N) で置き換えて得られるグラフは G のインスタンス である.
どんなグラフもそれ自身のインスタンスであり, G のインスタンスのインスタンスも G のインスタンスであり,
もし H が G のインスタンスなら H 中のどのトリプルも G のどれかのトリプルのインスタンスであることに注意されたい.
語彙 V に関するインスタンスとは,
元のグラフ中のブランクノードが置き換えられたインスタンス中のすべての名前が,
V からの名前であるようなインスタンスのことである.
あるグラフの真の (proper) インスタンスとはその中のあるブランクノードがある名前で置き換えられるか,
グラフ中の二つのブランクノードがそのインスタンス中の同じノードに写像されたようなインスタンスのことである.
あるブランクノードが元のグラフにはない新しいブランクノードに写像されるようなグラフのどんなインスタンスも,元のグラフのインスタンスであり,
またその元のグラフをインスタンスとして有する.そしてこの処置は繰り返され得るので,ブランクノード間の1:1写像は
元のグラフをインスタンスとするようなグラフのインスタンスを定義する.そのような二つのグラフ,互いに他のインスタンスであるがブランクノードだけが一致しない,
真のインスタンスではないようなグラフは等価と考えられる.
我々はそのような等価なグラフを同一のものとして扱う.そうすることにより,ノードIDの「改名」によって引き起こされるいくつかの問題を無視することができ,
ブランクノードはラベルを持たないという約束事に適合させることができる.
等価グラフは相互に可逆なインスタンス写像を有する二つのインスタンスである.
もしある RDF
グラフがその真部分グラフであるようなインスタンスを持たないならば,それは簡約 (lean) である.非簡約 (non-lean)
なグラフは内部に冗長性を有し,同じ内容をその簡約な部分グラフで表現することができる.例えば,グラフ
<ex:a> <ex:p> _:x .
_:y <ex:p> _:x .
は簡約ではないが,
<ex:a> <ex:p> _:x .
_:x <ex:p> _:x .
は簡約である.
RDF グラフ集合のマージ
は次のように定義される.もし集合中のグラフが共通のブランクノードを持たないなら,そのグラフの合併はマージである.
もしブランクノードを共有するなら,その集合中のグラフをブランクノードを共有しない等価なグラフに置き換えてグラフ集合の合併をとる.
これはしばしばブランクノードの「標準化分離 (standardized apart) 」と言われる.いかなる二つのマージも等価であることは容易にわかるので,
等価グラフの習慣に習って我々はそれに定冠詞をつけて the マージと言う.等価グラフと同一視の約束にしたがって,
元の集合中のどんなグラフもそのマージの部分グラフと考えられる.
一般に,グラフ集合に相当する N-トリプル文書を単純に連結して,
そのマージされた文書で記述されるグラフを構成しても,そのグラフのマージは得られない.もし文書のいつくかが同一のノード指定子を使っていたら,
そのマージされた文書はブランクノードが「偶然」同じであるようなグラフを記述してしまう.
N-トリプル文書をマージするには,
二つあるいはそれ以上の文書で同じノード指定子が使われていないかチェックして,
必要であれば文書をマージする前に個々のノード指定子を異なったものに置き換える必要がある.
同様な注意はノード指定子を含む RDF/XML 文書によって記述されるグラフをマージする際にも適応される.
RDF/XML Syntax Specification (Revised) [RDF-SYNTAX]
を参照のこと.
RDF はプロパティの定義域 (domain) と値域 (range) にいかなる論理的制約も課さない.特に,あるプロパティをそれ自身に適用してもよい.
クラスが RDFS で導入されるとき,それら複数のクラスがそれら自身を含んでもよい.
そのような「メンバーシップループ」は,基礎の公理であるところの,メンバーシップについて無限の降下の連鎖を禁止するという,標準 (Zermelo-Fraenkel)
集合論理の公理に違反するように見えるかもしれないが,ここで与えられる意味論的モデルでは,
オブジェクトとしてのプロパティとクラスはそれらの 外延 (extensions) -
そのプロパティを充足するオブジェクト・値ペアの集合や,そのクラスの「中」に含まれるような事物 - とは区別される.
それによって,基礎の公理に違反することなくあるプロパティとクラスの外延がプロパティやクラス自身を含むことができる.
特に,クラス外延写像を用いて,クラスがそれ自身を含むことができる.
例えば,ある「ユニバース」クラス(の外延)がメンバーとしてそのクラス自身を含むことは全く問題なく,
これはあるクラス階層のしばしば採用される約束事である.(もしある外延がそれ自体を含めば公理違反となるが,そのようなことは決して起こらない.)
このテクニックはより完全に [Hayes&Menzel ] に述べられている.
この点において,RDFS は個物の構造化された階層を仮定する UML
や個物の集合など,あるいはデータとメタデータの間ではっきりした違いのあるような,多くの通常のオントロジーの枠組みとは異なるものである.とは言え,RDFS
はそのような構造の存在を仮定しない一方で,それを禁止もしない.RDF はメンバーシップループを許すが,ユーザの語彙のすべての部分に対してその使用を強制はしない.
もし RDFS のこの側面が心配ならば,多くの実際の目的のために RDFS の表現力を得つつ,
クラスのメンバーシップやプロパティの適応についてそのような「ループ」を含まないような RDF グラフの部分集合に自ら制限することは可能である.
そして意味論的拡張をそのようなループ構造を禁止した構文論的諸条件と重ね合わせてもよい.
明示的な外延写像の使用はまた二つのプロパティが異なるエンティティでありながら,厳密に同じ値を持つことを可能にするし,
二つのクラスが同じインスタンスを含むことを可能にする.これは RDFS のクラスは単なる集合以上のものと考えられるということ意味している.
それらは単なる外延的一致を超えた,ロバストな同一性概念である
「分類 (classification) 」あるいは「概念 (concept) 」と考えられる.このモデル理論の性質は
RDF の上に構築されるより表現力のある言語,たとえばOWL [OWL] のような言語において顕著な結果をもたらす.
そこではプロパティとクラスの間の同一性を直接表現することができる.クラスとプロパティの「内包的」
特徴は時に記述的な言語の有益な性質であると主張されるけれども,その十分な考察は本文書の範囲ではない.
あるクラスがメンバーとしてそれ自身を含むか否かという問題は,それがそれ自身のサブクラスか否かという問題とは全く異なるということを注意しておく.
すべてのクラスはそれ自身のサブクラスである.
通常の論理的意味論に通じた読者は,RDF を,限量化されたユニバースにおいて関係が第1級のエンティティであるような,
存在限量された2項関係の翻案であると知ることが役に立つかも知れない.そのような論理は3値関係 トリプル(a,R,b) の記法から,
関係のアトム R(a,b) を通常の論理シンタックスとしてコード化することで得られる.ここで記述される基礎的な意味論は,
y の外延を集合{<x, z> : トリプル(x, y, z)} として定義して,
元の形式 R(a, b) の関係アトムを通常の Tarskian モデル理論における表示 (denotation) であるとすることで,
直感的に再構成することができる.この再構成はまた Lbase 公理的記述 [LBASE]
意味論においても確かめられている.
本文書では URI 参照が他の表現,例えば,相対 URI や QName などから構成される方法についてどんな立場もとらない.
意味論ではそのような字句的な問題は,グローバルに整合的な何らかの方法で解決されていると,単に仮定している.そのため,一つの
URI 参照はそれが起きるときにはいつでも同じ意味をとることができるとしている.同様に,意味論には時間的変化を追跡するようなどんな特別な用意もない.
URI 参照はそれが生起するときはいつでも 同じ意味であるということを仮定している.時間変化に敏感な意味論を適切に提供することは,
本文書の範囲を超えた研究課題である.
意味論では URI 参照が表示するものと,HTTPプロトコルにおいて URI
参照を用いて引き出される文書やウェブの資源,あるいはそのような文書のソースであると思われるエンティティとの間にどんな特別な関係も仮定しない.
そのような要求は意味論的拡張として付け加えられてもよいが,ここで述べられる形式的意味論においては,そのような
URI 参照の表示物と他のプロトコルにおいてそれら URI 参照を用いることの間にどんな関係も仮定しない.
意味論ではすべての RDF の名前をそれが表示するものの表現であるとしている.
表示されたものは [RFC 2396] にしたがって「リソース」と呼ばれるが,
リソース の本質については何も仮定されていない.
ここでは「リソース」とは「エンティティ」,すなわち論議の領域 (universe of discourse) における何かを表現する一般的な用語,
の同義語として扱われる.
名前の構文的に異なる複数の形式が,それぞれ個別に扱われる.URI 参照は単に論理定数として扱われる.
プレーンリテラルはそれ自身を表示するものと考えられ,その意味は固定である.
型付きリテラルが表示するものは,その型にちなんだデータ型によって写像されるその文字列の値である.
RDF では rdf:XMLLiteral で型付けされたリテラルに個別の意味があり,
それは第 3 節で記述されている.
モデル理論的な意味論とは,直感的に述べれば,ある文を表明するということは世界についての何かを主張する,
ということであり,それは,その文が真であるとする解釈があるべく世界は配置されていることの別の言い方である.
言い換えれば,表明とは世界のあり方の可能性 に関する制約 を述べることと同然である.
単一で唯一の解釈を明記するに十分な情報を表明が含んでいるなどということは,ここでは仮定されていないことを注意しておく.
どんな言語でも,表明によりたった一つの世界の解釈しかあり得ないように完全に制約するなどということは,普通は不可能である.
それゆえ,RDF グラフの「その」唯一の解釈というようなものはない.一般的に言えば,RDF グラフが大きければ大きいほど,
世界について多く言っていることになり,グラフのある表明が真である解釈の集合はより小さくなり,
表明されたグラフを真とする世界のあり方の可能性はより少なくなる.
解釈に関する以下の定義は数学の言語により言い表されるが,それが帰するところは,直感的には解釈とはいかなる基底 RDF トリプルについても
その真偽値(真または偽)を決めるための世界の可能なあり方,可能世界,についてちょうど十分なだけの情報を供給するようなものであるということである.
それは URI 参照に対しては名前で想定されるあるものを指定し,もしそれがプロパティを指すのであれば
その ユニバースにおける各事物に対してプロパティが持つ値を指定し,
もしそれがデータタイプを指定するならそのデータタイプが定義する
字句の形式とデータタイプの値との間の写像が定義されていることを指定することで行われる.
これはいかなる基底トリプルについてもその真偽値を決めるに十分な情報であり,
それゆえいかなる基底グラフについても十分である.(非基底グラフは以下の節で考察される.)もしこれらの情報のどれが省略されたとしても,
値が決まらないwell-formedなトリプルが残ってしまうかも知れず,
ユニバース中の事物の正確な性質といった,他のどんな情報もまた,
その本質的関係がどうあろうとトリプルの実際の真偽値とは無関係になってしまうかも知れないということを注意しておく.
すべての解釈は,解釈の語彙 (vocabulary) と呼ばれる名前の集合に呼応しており,
厳密には RDF それ自身というよりも RDF 語彙の解釈について語られるべきである.ある特定の語彙におけるシンボルに特別の意味を割り当てる解釈があってもよい.
ある特定の語彙の特別な意味を共有する解釈は,その語彙に対して,たとえば,「rdf-解釈」とか
「rdfs-解釈」などと名前が付けられる.
ある(RDF 語彙自身を含む)語彙に関して何ら特定の余分な条件がないような解釈は単純 解釈,あるいは単に解釈と呼ばれる.
RDF
ではいくつかのリテラル形式を用いる.リテラルの主な意味論的特徴は,その意味が含まれる文字列の形式によってほとんど決定されるということである.
埋込みの型 URI 参照がないプレーンリテラルは,文字列であってもあるいは
文字列と言語タグのペアであっても,
常にそれ自身を参照するものと解釈される.いずれの場合も,その文字列は「リテラル文字列」として参照される.しかし,型付きリテラルの場合には,
その意味の完全な明細は RDF 自体の外にあるデータタイプ情報にアクセス可能であるかどうかに左右される.
型付きリテラルの意味の完全な議論は第 5 節で述べられ,データタイプの解釈の特定の概念が紹介される.
各解釈では,型付きリテラルからその解釈への写像 IL が定義される. IL のより強い条件はあとの節において拡張される「解釈」の概念として定義されるであろう.
本文書を通じて,詳細な意味論上の条件が表として提示される.表には意味論的条件が述べられ,
真となる宣言と 正当な (valid) 推論ルールが含まれ,シンタックスが箇条書きされる.
その表は背景色で区別される.これら複数の表は,全部一緒にして,全体の意味論の正式な要約となる.RDF 意味論は RDFS 意味論に依存しないことに注意されたい.
RDF 意味論のすべては第1節と第3節で定義される.
RDFS 意味論のすべては 第1節, 第3節および第4節で定義される.
単純解釈の定義
|
語彙 V の単純解釈 I の定義は以下のとおり:
1. リソースの空でない集合 IR , これは I のドメインあるいはユニバースと呼ばれる.
2. 集合 IP ,これは I のプロパティの集合と呼ばれる.
3. IP から冪集合 IR × IR すなわち IR 中の x と y のペア <x,y> の集合の集合への写像 IEXT .
4. V 中の URI 参照から (IR union IP) への写像 IS .
5. V 中の型付きリテラルから IR への写像 IL .
6. リテラル値の集合と呼ばれ,IR の部分集合として識別される LV , これには V
中のすべてのプレーンリテラルが含まれる. |
IEXT(x) は x の外延 (extension) と呼ばれ,
ペアの組み合わせについてそのプロパティに対して真であるようなペアの集合,すなわち2項関係の外延である.
オブジェクトとしての関係とその外延を区別するというトリックによって,既に述べたように,
あるプロパティがそれ自身の外延中にあってもよいようになる.
LV は IR の部分集合とすることによって,リテラル値が本当にエンティティとして「存在」すると言ってもよいことになる.
すなわち,リテラル値はリソースであると言ってもよいことにもなる.しかしこれは,リテラルが URI 参照で同定されなければならないという意味ではない.
LV はプレーンリテラルに加えて,他の項目を含んでよいことに注意されたい.IL の値域を LV に制限するのではなく IR にしたのには技術的な理由がある.
データタイプ情報を解釈するとき,構文論的には型付きリテラルが最初矛盾する (inconsistent) 可能性があり,
第5節で説明するように,
そのような悪い型付けのリテラルが非-リテラル値を表示するのに必要だからである.
次節では,どのようにして語彙の解釈が,いかなる RDF グラフの真偽値でも,その表示すなわち意味的な「値」をその直接の下位表現の項における表示の
再帰的定義によって決定するかを定義する.これはこの次の後継となるすべての意味的拡張にも適用される.
RDF に二種類の表示的意味があり,名前はユニバースにおける事物を表示し,トリプル集合は真偽値を表示する.
I において基底 RDF グラフが表示するものは次のルールによって再帰的に与えられる.
それは名前から基底グラフへの解釈写像 I を拡張したものである.これらのルール(と後で述べるそれらの拡張)は,
RDF 構文のどんな断片 E についても,E の各構文論的構成要素がじかに表示する物から E の表示物を定義するように作用する.
それ故,一種の構文的な再帰によって RDF のどんな断片についてもその意味を定義することができる.
以下の表と本文書を通じて,等号=は同一性を表し,かぎ括弧 <x,y> は x と y の順序ペアを表す.RDF グラフ構文は RDF テストケース文書 [RDF-TESTS] に記載された N-トリプル の記法を用いて表される.
リテラル文字列は二重引用符ではさんで表示され,言語タグは @ 記号を用いて表示され,トリプルは「コードドット」. で終わる.
基底グラフに対する意味論的条件
| もし E が V におけるプレーンリテラル "aaa" ならば,I(E) = aaa である |
もし E が V におけるプレーンリテラル "aaa"@ttt ならば,I(E) = <aaa, ttt> である |
| もし E が V における型付きリテラルならば,I(E) = IL(E) である |
| もし E が V における URI 参照ならば,I(E) = IS(E) である |
|
もし E が V における基底トリプル s p o. ならば,s,p そして o が V 中にあり,
I(p) は IP 中にあり <I(s),I(o)> が IEXT(I(p)) 中にあれば,I(E) = 真
さもなければ I(E) = 偽 である. |
| もし E が基底グラフならば,E 中のあるトリプル E' に対して I(E') = 偽 となる E'
があれば I(E) = 偽 ,さもなければ I(E) = 真 である. |
もし RDF グラフの語彙が解釈 I の語彙にはない名前を含むなら,すなわち,もしそのグラフ中で用いられたある名前に,
単純に意味論的な値がただ与えられないのなら,これらの真偽条件は常にグラフ中のあるトリプルに,それゆえそのグラフ自身にも,偽を生成するであろう.
ひるがえって,これはグラフ中のどんな表明もそのグラフ中のすべての名前は,実際世界の何かを指すということである.
上記最後の条件は空グラフ(トリプルが空の集合)は真ということを意味する.
プレーンリテラルの表すものは常に LV 中にあること,そしてどんな真であるトリプルのサブジェクトとオブジェクトも IR 中にあることを注意しておく.
だから,あるグラフ中にプレディケイトとしてもサブジェクトあるいはオブジェクトとしても現れる URI 参照は
そのグラフを充足するどんな解釈においても IR と IP の共通集合中の何かを表示しなければならない.
説明の例として,人工的な語彙 {ex:a, ex:b, ex:c, "whatever", "whatever"^^ex:b}
に対する小さな解釈を以下に掲げる.そのユニバースにおける非リテラルな「物」を指すのに整数を用いる.
これは解釈は数学的に解釈されるべきであるという意味ではなく,ユニバース中の物の性質とは無関係であるということをより強調するためのものである.
LV はその意味論的条件を満たす集合であればなんでも良い. (これと引き続きの例において,greater-than と less-than
シンボルは複数の目的のために用いられる.すなわち抽象ペアと N トリプルを指す場合,N トリプル構文論にしたがって URI
参照を囲む場合,そして写像を示すときの矢印としての場合である.)
IR = LV union {1, 2}
IP={1}
IEXT: 1=>{<1,2>,<2,1>}
IS: ex:a=>1, ex:b=>1,
ex:c=>2
IL: "whatever"^^ex:b =>2
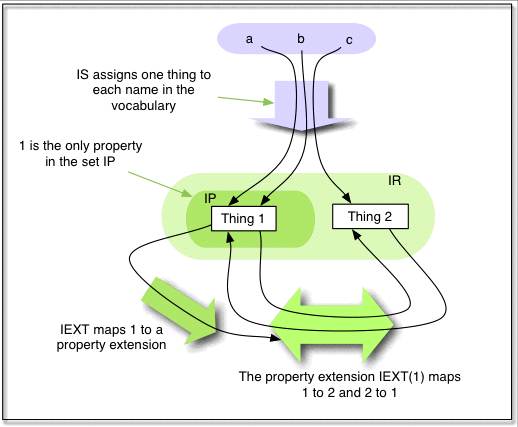
Figure 1:
ある解釈例.これは RDF グラフの絵ではないことを注意しておく.
この図は LV の無限個のメンバーを示してはいない.
この解釈は次のトリプルを真とする.
<ex:a> <ex:b> <ex:c> .
<ex:c> <ex:a> <ex:a> .
<ex:c> <ex:b> <ex:a> .
<ex:a> <ex:b> "whatever"^^<ex:b>
.
例えば,もし <I(ex:a),I(ex:c)> が
IEXT(I(<ex:b>)) 中にあれば, すなわち,もし <1,2> が IEXT(1) 中にあれば,
I(<ex:a> <ex:b> <ex:c> .) = 真 である.何故ならば IEXT(1) は
{<1,2>,<2,1>} でそれは <1,2> を含んでおり,それは I(<ex:a
<ex:b> ex:c>) であるから.
4番目の トリプル の真は,どちらかと言えば型付きリテラルに対してここで選択された固有の解釈の結果である.
この解釈において IP は IR の部分集合であり,それは RDF 意味論解釈では典型的ではあるが,必ずそうというわけではない.
つぎのトリプルは偽となる.
<ex:a> <ex:c> <ex:b> .
<ex:a> <ex:b> <ex:b> .
<ex:c> <ex:a> <ex:c> .
<ex:a> <ex:b> "whatever" .
例えば,もし <I(ex:a), I(<ex:b>)> すなわち
<1,1> が IEXT(I(ex:c)) 中にあれば I(<ex:a> <ex:c>
<ex:b> .) = 真 であるが, I(ex:c)=2 は IP 中にはなくて,2 に関して IEXT
は定義されていないからその条件は失敗して I(<ex:a> <ex:c> <ex:b> .) =
偽 となる.
そのプロパティ外延はプレーンリテラルを含むどんなペアも含むことはないので,プレーンリテラルを含むすべてのトリプルは偽となる
これはこの語彙のひとつの可能な解釈に過ぎないということを強調しておく.たとえば,もしこの解釈が,そのプロパティ外延が1ではなく2であるように修正されると上記トリプルで真となるようなものはない.
この例はグラフのトリプル中のプレディケイトの位置にくるようなどんな URI 参照も IP 中にはないものに写像されるような解釈は,そのグラフを偽とするということを示している.
ブランクノードはその物の名前を使ったり,何かを言ったりすることなく,ただ単に物の存在を示すものとして扱われる.(これはブランクノードが「未知な」URI
参照を指すということではない.たとえば,その物を参照する URI 参照があるということではない.付録 A にある スコレム化
の議論がこの点と関連する.)
解釈はブランクノードを含むグラフの真偽値を特定できる.ここまでの理論ではブランクノードについて何の意味も提供してこなかったので,それには何か新たな定義が必要である.
I は解釈で A はブランクノードのある集合から I のユニバースへの写像だとしよう.そして I+A をある拡張解釈,ブランクノードの解釈を与えるそれを除いたら
I となるような拡張解釈,とする. blank(E) を E
中のブランクノード集合と定義する.すると上記ルールはグラフ中にブランクノードがあるとき,次の二つの新しいルールを含むように拡張される.
ブランクノードに対する意味条件
| もし E がブランクノードで,かつ A(E) が定義されていれば, [I+A](E) =
A(E) |
| もし E が RDF グラフならば,blank(E) から IR へのある写像 A' に対して,
[I+A'](E) = 真 ならば I(E) = 真 ,さもなければ I(E) = 偽 |
これは解釈の定義を変更はしないということに留意されたい.それは依然として同じ IR,IP,IEXT,IS,LV,IL
の値から構成されている.それはただ単にある解釈のもとで基底グラフに対する真偽値を提供する解釈が,たとえブランクノード自身の解釈を提供しなくても,
ブランクノード付きのグラフにも真偽値を当てられるように表示物の定義のためのルールを拡張するだけである.ブランクノード自身は完璧に well-defined
なエンティティであることにも留意されたい.それは解釈による表示物が与えられないということだけが,他のノードとは異なっている.
これはブランクノードには「グローバル」な(すなわちブランクノードが含まれるグラフの外側では)意味がないという直感の反映である.
例えば,次のトリプルによって定義されるグラフは figure 1
に示された解釈では 偽 である.
_:xxx <ex:a> <ex:b> .
<ex:c> <ex:b> _:xxx .
何故ならば,もし A' がそのブランクノードの 1 への写像とすると,1番目のトリプルは I+A' 中で偽となるし,もしそれが 2 への写像とすると,
2番目のトリプルが偽となるからである.
これらのトリプル各一つを単一のグラフと考えれば,それはそれぞれ I
中で真となることに注意されたい.しかし,全体としてはそうではない.そしてもし二つのトリプルで異なるノードIDが用いられて,一個ではなく二つのブランクノードを有する
RDF グラフであったなら,A' は一つのノードを 2 に,他の一つを 1 に写像することができて,その結果グラフは解釈 I の下で真となることができる.
このことは,ブランクノードを有する RDF グラフにおいて,グラフ全体をスコープとして,
すべてのブランクノードを効果的には存在限量変数と同じ意味として扱うということである.
N トリプル構文における表現においては,これは要するに,限量子をグラフに相当する N トリプル文書の外部に置くという便法と同じことである.
その反面,二つのグラフのユニオンを作るという操作とマージするという操作の間に
微妙なしかし重要な区別があるということになる.
二つのグラフの単純なユニオンは,両方のグラフに含まれるどんなブランクノードでもその同一性を保ったままの,
グラフ中のすべてのトリプルの連言(conjunction, and)に相当する.これはグラフ中の情報が一つの情報源からもたらされる場合,すなわち,
例えばある推論ルールがグラフにトリプルを追加するなどといった,
片方がもう片方から何らかの正当な推論プロセスによって導かれるような場合には適切である.
二つのグラフをマージするということは,それぞれのグラフ中のブランクノードをそのグラフ中で存在限量されているように扱うということであり,
一つのグラフのブランクノードを他のグラフを囲む限量子のスコープに迷い込ませるということは許されない.
これはグラフが異なる情報源からもたらされる場合でかつ片方のグラフ中のブランクノードがもう片方のグラフ中のブランクノードと
同じエンティティを参照しているという証拠がない場合に,適切である.
これまでの用語の慣習にしたがって,もし I(E) = 真 ならば I は E を充足する という.もしもある RDF グラフ集合 S
のどのようなメンバーも充足するどのような解釈もまたあるグラフ E を充足するのなら,S は E を(単純に) 伴意する
という.後述する節において,この概念が解釈の他のクラスに適応されるが,この節においては「伴意」とは単純伴意として理解されるべきである.
伴意はモデル理論としての意味論を現実世界の応用に結合するのに決定的な鍵となるアイデアである.先に述べたように,表明するということは表明に真を割り当てる解釈を世界について主張するということである.もし
A が B を伴意するのなら,A を真とするどのような解釈も B を真とする.したがって,A の表明はすでに B の表明と同じ「意味」を含んでいる.B
の意味はとにもかくにも A の意味に含まれている,あるいは包摂されていると言ってもいいかもしれない.もし A と B
がお互いを伴意するのなら,どちらかを表明することは世界について同じ事を主張するという点で,それらは同じことを「意味」する.この所見でもっとも鮮明に面白いことは,
A と B
の表現が異なるときである.そのときの伴意の関係は,あるアプリケーションが片方からもう片方を推論するあるいは生成することを正当化するための,まさに適切な意味論的許可証となる.充足性,伴意,そして正当性の概念を通じて,形式的意味論は「意味」の概念に厳密な定義を与え,知識の表現に関する変換によって意味が保存されるか否かを決定する計算手法に直に関係している.
あるグラフ E を何か別のグラフ S
から構成する過程は,すべての場合に もし S が E を伴意するのなら,(単純に)正当である と言われる.
さもなければ非正当である.非正当な過程であるということはその結論が偽であるということを意味しないし, 正当であることが真を保証するのでもないということを注意しておく.しかしながら,正当性は宣言型言語が提供できる最良の保証を表現する.もし真の入力が与えられれば,その結果として偽が導かれることはけっして無い.
この節では単純伴意と正当な推論について,2,3
の基礎的な結論を与える.単純伴意は,比較的単純な構文上の比較対照により認知できる. RDF における単純に正当な推論の二つの基礎式は,論理表現すれば,(P
and Q) から P を推論することと, foo(baz) から (exists (?x) foo(?x)) を推論することである.
これらの結論は単純伴意のみにしか適応されず,後述の節で導入される伴意の拡張概念には当てはまらない.証明は,すべて複雑ではないが,付録
Aにあり,興味ある他の伴意の性質も記述してある.
空グラフのレンマ. トリプルの空集合はいかなるグラフによっても伴意され,それ自身以外のいかなるグラフも伴意しない. [Proof]
サブグラフのレンマ. グラフはそのサブグラフをすべて伴意する.
[Proof]
インスタンスのレンマ.
グラフはそのいかなるインスタンスによっても伴意される. [Proof]
マージと伴意との関係は,その定義より簡単かつ明白である.
マージのレンマ. RDF グラフの集合 S のマージは S
によって伴意され,S のどのメンバーも伴意する.[Proof]
これは,グラフの集合はモデル理論に関する限りではそのマージと,すなわち一つのグラフとして,等価に扱ってよいということを意味している.これは用語の使い方を簡単にするのにいくらか役に立つ.例えば,上記のように,S
の定義が E を伴意する,というのは S を充足するすべての解釈が E も充足するとき,S が E を伴意すると言い換えることができる.
1.5 節に示された例はそうではないが,一般的には,グラフ集合の単純なユニオンはその集合によって伴意される.
単純 RDF 推論に対する主な結果は以下のとおり.
内挿レンマ. S は,もしそのあるサブグラフが E
のインスタンスであるならば,またそのときに限り,グラフ E を伴意する.[Proof]
内挿レンマは単純 RDF 伴意を構文上の考え方として完全に特徴付ける. RDF グラフのある集合が別のグラフを伴意するかどうかわかるためには,
もとのグラフ集合のマージの部分集合となる伴意グラフのインスタンスの存在をチェックすればよい. もちろん,本当にマージを構成する必要はない.帰結
E から逆向きに考えるのなら,効率的な手法があって,サブグラフ・マッチングの過程においてブランクノードを変数として扱って,帰結
グラフを伴意しそうな, S 中の前件
グラフの名前に「マッチ」するように束縛させればよい.もしサブグラフ・マッチングのアルゴリズムさえ正しければ,内挿レンマはこの過程を正当かつ完全なものにする.
完全なサブグラフ・マッチングのアルゴリズムがあれば,また
RDF 伴意が決定可能であること,すなわちいかなる有限集合 S といかなるグラフ E に対しても S が E
を伴意するかどうか決めることができるような,停止するアルゴリズムがあるということになる.
そのような変数束縛過程は提案された伴意の結論
に適応されるときにのみ適切である.これは文書を表明すなわちそれが真であると主張するのではなく,ゴールあるいはクエリとして用いることに等しい.もしある RDF
文書が表明されたのなら,その結果であるグラフは表明によって正しくないかも知れないので,ブランクノードのいずれかを新しい値に束縛しても非正当であるかも知れない.
内挿レンマから非伴意に関するクライテリアが直接的に結論される.
匿名性レンマ. E はある 簡約な グラフで,
E' は E の真のインスタンスだとしよう.そのとき E は E' を伴意しない.[Proof]
再び,これは単純伴意にのみ適応されることを注意しておく.この文書の残りで定義される語彙の伴意関係には適応されない.
伴意に関するいくつかの基本的性質が上記定義から直接導かれるが,完全を期してここで述べておく.
単調性レンマ. S
を S' のある部分グラフとして,S は E' を伴意するとすると,そのとき S' は E を伴意する. [Proof]
前提条件の有限集合から通常導かれる有限な表現に関する性質はコンパクト性 (compactness)
と呼ばれる.伴意の非コンパクト概念を支持するセマンティック理論は計算可能な推論システムとは対応しない.
コンパクト性レンマ.もし S が E
を伴意して,E が有限グラフならば,E を伴意する S の有限部分グラフ S' がある.
2.1
語彙の解釈と語彙の伴意
単純解釈と単純伴意は,グラフ中の名前に特有な意味について何ら注意しないときに得られる RDF グラフの意味論である.特定の語彙を用いて書かれた RDF
グラフの意味を全部得るためには,普通はグラフ中の特定の URI
参照と型付きリテラルにより強い意味を付与する意味論的条件をさらに追加することが必要である.特定の語彙に関する特別の意味論的条件を満足させる解釈は,一般的に語彙解釈
(vocabulary interpretation)
と呼ばれる.語彙伴意とは,そのような語彙の解釈に関する伴意のことである.このような解釈のより強い概念は名前空間のプレフィックスを用いて示され,以下において,rdf-伴意
とかrdfs-伴意 などのように呼ばれる.各々の場合において,意味が制限された語彙と語彙に関連する特別な条件が詳細に記述される.
RDF 語彙,rdfV,は rdf:
名前空間における URI 参照の集合である.
| RDF 語彙 |
rdf:type
rdf:Property rdf:XMLLiteral rdf:nil rdf:List
rdf:Statement rdf:subject rdf:predicate rdf:object rdf:first rdf:rest
rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2 ...
rdf:value |
rdf-解釈は
rdfV
と, RDF にビルトインされたデータタイプであるが,型 rdf:XMLLiteral
で型付けされたリテラル,に特別な意味条件を重ね合わす.このデータタイプについてはRDF Concepts and
Abstract Syntax 文書 [RDF-CONCEPTS]
中に 完全に記述されている.
rdf:XMLLiteral
の字句空間に記述されている条件を満たす文字列 sss は well-typed XML リテラル文字列
と呼ばれる.その対応する値はリテラルの XML 値 と呼ばれる. well-typed XML リテラルの XML
値は,正確にそのようなリテラルの XML リテラル文字列と 1 対 1 対応しているが,それ自身は文字列ではない.そのリテラル文字列が
well-typed であるような XML リテラルは, well-typed XML リテラルと呼ばれ,それ以外のリテラルは
ill-typed と呼ばれる.
語彙 V の rdf-解釈
は,以下の表に記述された特別条件と,引き続く表中のすべてのトリプルを満たす (V union rdfV)
の単純解釈 I である. これらトリプルは RDF 公理トリプル と呼ばれる.
RDF 意味論的条件
|
もし <x,
I(rdf:Property)> ∈ IEXT(I(rdf:type)) ならば,
そしてその時に限り,x ∈ IP . |
|
もし
"xxx"^^rdf:XMLLiteral ∈ V かつ xxx が
well-typed XML リテラル文字列ならば,
IL("xxx"^^rdf:XMLLiteral) は xxx の XML
値;
IL("xxx"^^rdf:XMLLiteral)
∈ LV;
<IL("xxx"^^rdf:XMLLiteral),
I(rdf:XMLLiteral)> ∈ IEXT(I(rdf:type)) .
|
|
もし
"xxx"^^rdf:XMLLiteral ∈ V かつ xxx が
ill-typed XML リテラル文字列ならば,
IL("xxx"^^rdf:XMLLiteral) は LV
中ではない;
<IL("xxx"^^rdf:XMLLiteral),
I(rdf:XMLLiteral)> は IEXT(I(rdf:type))
中ではない. |
最初の条件は,IP
をプロパティ I(rdf:type) の値,I(rdf:Property)
を有する解釈のユニバース中のリソース集合として定義するというように見做すことができる.そのようなユニバースの部分集合が RDFS の解釈の中心となる.この条件は
IP が IR の部分集合であることを要請することに注意されたい. 三番目の条件は,ill-typed
XML リテラルがリテラル値以外のものを表示することになり,これが ill-formed な型付きリテラルを扱う標準的な方法である.
RDF 公理トリプル.
rdf:type rdf:type rdf:Property
.
rdf:subject rdf:type rdf:Property .
rdf:predicate rdf:type
rdf:Property .
rdf:object rdf:type rdf:Property .
rdf:first rdf:type
rdf:Property .
rdf:rest rdf:type rdf:Property .
rdf:value rdf:type
rdf:Property .
rdf:_1 rdf:type rdf:Property .
rdf:_2 rdf:type
rdf:Property .
...
rdf:nil rdf:type rdf:List
. |
第4節以下で記述される
rdfs-解釈は,
RDF 語彙で用いられるプロパティにさらに意味論的条件 (値域と定義域条件)を割り当てるが,この節で記述された条件に適合しなければならない
条件を供給することで,他の意味論的拡張によりそれらの意味をさらに制限するような条件をさらに重ね合わせても よい.
例えば,以下の rdf-解釈は figure 1 の単純解釈を V が rdfVを含む場合に拡張している.
この例では簡単のために,XML リテラルは無視した.
IR = LV union {1, 2, T , P}
IP = {1, T}
IEXT: 1=>{<1,2>,<2,1>},
T=>{<1,P>,<T,P>}
IS: ex:a=>1, ex:b=>1, ex:c=>
2, rdf:type=>T, rdf:Property=>P,
rdf:nil=>1, rdf:List=>P,
rdf:Statement=>P, rdf:subject=>1,
rdf:predicate=>1, rdf:object=>1,
rdf:first=>1, rdf:rest=>1,
rdf:Seq=>P, rdf:Bag=>P,
rdf:Alt=>P, rdf:_1, rdf:_2, ... =>1
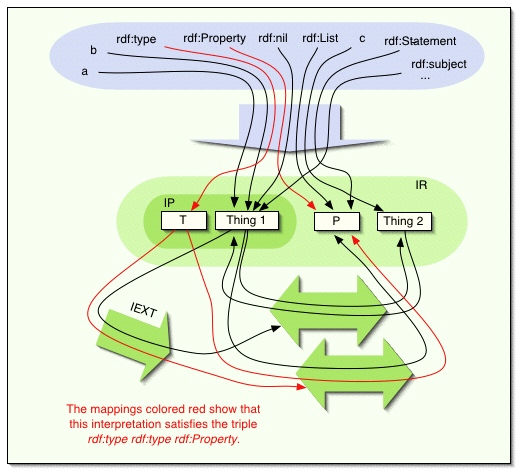
Figure 2: ある
rdf-解釈.
IEXT(T) を {<1,2>,<T,2>} として,ユニバース中に P を取り込まなくすることができるので,この例は先の例を拡張した最小
rdf-解釈ではない.一般に,ある解釈中に与えられたエンティティは要求された意味論的条件に違反しないかぎりにおいて,同時にいくつかの '役割'
を果たすことができる.たとえば,上記解釈はプロパティをリストにより同定するが,もちろん別の解釈はそのような同定ではないかも知れない.
どんな rdf-解釈 も単純解釈である. '特別な' 構造が単純な役割を演じることを妨げはしない.
3.2. RDF 伴意
S のどのメンバーも充足するすべての rdf-解釈が E も充足させるとき,S は E を rdf-伴意 する.この言い方は第2節の
単純伴意の言い方に倣っただけであるが,単純解釈のかわりにrdf-解釈と言い換えている.
Rdf-伴意は語彙伴意の一例である.
第2節におけるレンマがすべて
rdf-伴意にも当てはまるわけではないということを見て取ることは容易である.たとえば,トリプル
rdf:type rdf:type rdf:Property .
はすべてのrdf-解釈において真であり,空グラフによって
rdf-伴意されて,rdf-伴意に対する内挿レンマと矛盾する. 7.2
節では RDF 伴意を検知するための厳密な条件を記述する.
RDF の意味論的条件は中心的な RDF 語彙の意味にのみ顕著な形式的制約を重ね合わすので,rdf-伴意やrdf-解釈が残りの語彙にさらに変化を引き起こすことはない.これにはコンテナと閉じられたコレクションを記述することが意図された語彙や,RDF
グラフの記述をトリプルで記述可能にするための具体化 (reification)
語彙が含まれる.この節では,この語彙の意図された意味についてレビューし,形式的モデル理論によって支持されない直感的結論について述べる.意味論的拡張はこれらの意図された意味に適合している語彙の形式的解釈を制限してもよい.
形式的意味論からこれらの条件を省略するのは現存の RDF 使用における変更に適応させて,形式的 RDF
伴意のチェックの実装工程をより簡単にするための設計上の決定である.例えば,実装では RDF
コレクション語彙の実装において特別な手続き的技術を用いることを決定してもよい.
| RDF reification 語彙 |
rdf:Statement rdf:subject rdf:predicate
rdf:object |
意味論的拡張がこれらの語彙の解釈を次のように制限してもよい.すなわち,トリプル式
aaa rdf:type rdf:Statement .
は丁度 I(aaa) があるRDF文書中のあるRDFトリプルのトークンであるとき,そのような表示されたトリプルに適応されたときに三つのプロパティがそのトリプルのそれぞれの構成要素と同じ値を持つときに真であると.
これは次の二つのRDFグラフを考えることで説明できる.最初は一つのトリプルであり,
<ex:a> <ex:b> <ex:c> .
そして二つ目は以下である.
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:a>
.
_:xxx rdf:predicate <ex:b> .
_:xxx rdf:object <ex:c>
.
この2番目のグラフは最初のグラフのトリプルの具体化と呼ばれ,
その最初のトリプルを参照することが意図されているノード - 2番目のグラフのブランクノード - は,紛らわしいことに,
具体化されたトリプル (reified triple) と呼ばれる (ブランクノードであってもURI参照であってもよい).
具体化語彙で意図された解釈では,2番目のグラフは,その具体化されたトリプルが,
ある実際のRDF文書中にある最初のグラフのトリプルのトークンを参照するように解釈されることで,解釈 I において真となる.
ただし,そのトークンは正しいRDF構文論だとして,I を用いてそのトークンがインスタンシエートする構文論的なトリプルを解釈して,
結果,そのトリプルのサブジェクト,プレディケイト,オブジェクトが具体化によって記述されたトリプルと同じ様に解釈されるものとしている.
このことは形式的には次のように述べることができるかも知れない.
<x,y> は x がRDFトリプル式
aaa bbb ccc .
のトークンで,かつ y が I(aaa) であるときに,以下プレディケイトとオブジェクトについてもそれぞれ同様であるときに,
外延 IEXT(I(rdf:subject)) の要素となる.
rdf:subjectプロパティの値はサブジェクトURI参照自体ではなくその解釈であり,
したがってこの条件は2段階の解釈のプロセスを含んでいるということを注意しておく.
すなわち,具体化されたノード - 具体化のトリプルのサブジェクト - が他のトリプルを参照するという解釈であり,
それからRDF構文論にしたがってそのトリプルを扱って,そのサブジェクトの表示物を得るためにもう一度解釈写像を適応する.
このことは,トリプルのトークンが,ある解釈のユニバース IR 中に第1級のエンティティとして存在するということである.
まとめると,具体化の意味は,最初のグラフが意味するものは何でも意味するようなトリプルトークンを含む文書が存在するということである.
この具体化語彙の理解の仕方は,引用の形式としての具体化の解釈ではなく,
具体化はトリプルのトークンとトリプルが参照するリソースとの間の関係を記述するものということである.
具体化は直感的言えば「このRDFの1個がこの式を持つ」というのではなく,「このRDFの1個はこれらのものについて語っている」と読むことができる.
ここでの意味論的拡張は,具体化されたトリプル - 上記例では I(_:xxx) - が,
特定のトークンすなわち(実際のあるいは想像上の)RDF文書におけるあるトリプルの実現体であって,
文法的形式としての '抽象的な' トリプルではない,ということである.
同じサブジェクト,プレディケイト,オブジェクトの性質を有するようなエンティティが複数あるかも知れない.
一つのグラフがあるトリプル集合として定義されていても,異なる文書中に同じトリプルの構造を有するようなトークンが複数あるということが起こりえる.
かくして,上記2番目のグラフ中のブランクノードが最初のグラフ中のトリプルを参照するのではなくて
同じ構造の何か別のトリプルを参照していると主張することも有り得る.この具体化に関する特別の解釈は,
構成の日付や由来情報のような性質を具体化されたトリプルに適応して,
特定のインスタンスすなわちあるトリプルのトークンを参照するためだけに意味があるように選択されたものである.
RDFの適応はRDF文書中のトリプルトークンを参照する具体化を使用するけれども,その文書とその具体化との関係は
いわゆるRDFグラフ構文論 (RDF/XML Syntax Specification (Revised)
[RDF-SYNTAX]中に記述された RDF/XML構文論では,rdf:ID 属性はあるトリプルの記述中で用いられて,
その中では具体化されたトリプルがそのXML文書のベースURIとフラグメントとしてのrdf:IDの値から構成されるURI
であるような具体化を生成することができる) の外部で何らかの手段によって保守されなければならない.
あるトリプルのある具体化の宣言が暗黙にそのトリプル自身を宣言するわけではないので,あるトリプルとその具体化の間で何の伴意関係も存在しない.
かくして,具体化語彙はそれらがrdf-解釈に適応されること以外には,意味論的制約にどんな効果ももたらさない.
トリプルの具体化はそのトリプルを伴意しないし,それによって伴意もされない. (具体化はそのトリプルトークンが存在してそれが何かを言うだけで,
それが真であると言うのではない.トリプルによってトークンが伴意されないというのは,
あるトリプルを宣言したからといって自動的にそのトリプルによって記述されるユニバース中にトリプルのトークンが存在することを宣言するのではない
ということの帰結である.たとえば,そのトリプルが動物に関するオントロジーの一部だとして,動物だけを含むユニバースにおける解釈によって充足させられて,
その具体化はそのユニバースにおいて偽となるかも知れない.)
いかなるRDFグラフ中のトリプルとトリプルの具体化との関係も,1対1の関係ではないので,
ある具体化に記述されたあるエンティティについての性質について宣言することが,その同じ性質が他のそのようなエンティティにも成立する,
たとえそれが同じ要素を持つとしても,ということを伴意しない.たとえば,
_:xxx rdf:type rdf:Statement .
_:xxx rdf:subject <ex:subject>
.
_:xxx rdf:predicate <ex:predicate> .
_:xxx rdf:object
<ex:object> .
_:yyy rdf:type rdf:Statement .
_:yyy rdf:subject
<ex:subject> .
_:yyy rdf:predicate <ex:predicate> .
_:yyy
rdf:object <ex:object> .
_:xxx <ex:property> <ex:foo>
.
は
_:yyy <ex:property> <ex:foo> .
を伴意しない.
| RDF コンテナ語彙 |
rdf:Seq rdf:Bag rdf:Alt rdf:_1 rdf:_2
... |
RDFでは三種類のコンテナクラスを記述するための語彙が提供されている.コンテナにはタイプがあって,そのメンバーはコンテナメンバーシッププロパティ
の決められた集合を用いて数え上げることができる.このプロパティはメンバーを互いに区別するために整数によってインデックス化されるが,それらインデックスは必ずしもコンテナ自身の順番を定義すると考えられているわけではない.ある種のコンテナには順番はないとされている.
この後で記述されるRDFS語彙において,位置に関係なく成立する総称メンバーシッププロパティと,
すべてのコンテナとすべてのメンバーシッププロパティを含むクラスが追加される.
このRDF語彙はコンテナを構成する語彙としてではなく,プログラム言語において典型的にあるように,コンテナを記述する
語彙として理解されるべきである.この見方において,実際のコンテナは意味論的なユニバース中のエンティティであり,その語彙を用いているRDFグラフは単にこれらのエンティティについて非常に基本的な情報を単に提供して,RDFグラフがコンテナのタイプとコンテナのメンバーについての部分的な情報を与えることが可能となる.RDFコンテナ語彙は非常に限られているため,RDFコンテナに関する数多くの
'自然な' 仮定が RDFモデル理論によって形式的に容認されるというのではない.これはそれらの仮定が偽であるという意味ではなく,単にRDFではそれらが真だと形式的に伴意できない,という意味である.
コンテナ語彙に関して特別な意味論的条件はない.コンテナが持つとRDFが仮定する '構造'
だけが,語彙の使用と一般的RDF意味論の条件から推論されるものである.一般に言って,これはコンテナのタイプを知るということと,
コンテナ中のアイテムの部分的な数え上げがあるということである.その意図された使用法はタイプrdf:Bagでは順序がなくて同じものが複数あってよく,
タイプがrdf:Seqのものは順序付けされていて,タイプがrdf:Altでは代替物のコレクションと考えられて,その選好に順番がある場合もある.
順序付けされたコンテナ中のアイテムの順序ではコンテナメンバーシッププロパティの重複しない数字の順番によって指定されものとしている.
しかしながら,このような非形式的解釈はいかなる形式的RDF伴意においても反映されていない.
RDFはrdf:Bagの要素を異なる順序で数え上げることから起こるどんな伴意も支持しない.たとえば,
_:xxx rdf:type rdf:Bag .
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_2
<ex:b> .
は
_:xxx rdf:_1 <ex:b> .
_:xxx rdf:_2 <ex:a> .
を伴意しない.
もしこの結論が正当とするならば,それを元のグラフに結合した結果もまた正当な伴意となろう.それは両方の要素が両方の位置にあることを宣言する.これはRDFが純粋な宣言型言語であることの帰結である.
コンテナの性質がコンテナのどの要素にも当てはまり,その逆もしかりという仮定はない.
三つのコンテナクラスが互いに素(disjoint)であるという形式的な要求はないために,たとえば
rdf:Bagにもrdf:Seqにも宣言されるということが有り得る.コンテナにはすきまがないという仮定はないので,たとえば,
_:xxx rdf:type rdf:Seq.
_:xxx rdf:_1 <ex:a> .
_:xxx rdf:_3
<ex:c> .
が
_:xxx rdf:_2 _:yyy .
を伴意するということはない.
RDFにはコンテナを 'クローズ'
する方法,すなわち固定のメンバー数を宣言する方法,はない.これはどんなコンテナのメンバーシッププロパティを宣言するグラフでも,それにトリプルをいつでも追加できて矛盾はないことの反映である.最後に,RDFコンテナが有限の数のメンバーを含むという仮定はもともとないということを述べておく.
3.3.3 RDF コレクション
| RDF コレクション語彙 |
rdf:List rdf:first rdf:rest
rdf:nil |
RDF はコレクションを記述するための語彙,すなわちhead-tail
リンクのリスト構造,を提供する.コレクションはコンテナとは異なって,分岐構造を許し,明示的な終端を有し,アプリケーションがコレクション中のアイテム集合を正確に決定することができる.
コンテナと同様に,この語彙にはrdf:nilのタイプはrdf:Listであること以外に特別な意味論的条件はない.コンテナであったらブランクノードを使って記述するところを,2種類のトリプル,
_:c1 rdf:first aaa .
_:c1 rdf:rest _:c2
.
ここで,最後のアイテムにはプロパティrdf:restの値としてrdf:nilが用いられる.よく知られた便法であるが,rdf:nilは空なコレクションと考えることができる.そのようなグラフはつまるところコレクションの存在の宣言であり,コレクションのメンバーを調べることができるので意味されているものが何なのかをアプリケーションが決定するには十分である.しかし,意味論的には,空コレクションも含めて,グラフ中に明示的に言及されること以外に何もないということに留意されたい.たとえば,二つのアイテムを含むコレクションがあるということが,自動的にアイテムが交換されたコレクションの存在を保証はしない.
_:c1 rdf:first <ex:aaa> .
_:c1 rdf:rest _:c2
.
_:c2 rdf:first <ex:bbb> .
_:c2 rdf:rest rdf:nil .
だからといって
_:c3 rdf:first <ex:bbb> .
_:c3 rdf:rest _:c4 .
_:c4
rdf:first <ex:aaa> .
_:c4 rdf:rest rdf:nil .
ではない.
また,この語彙の使用にRDF が 'well-formedness'
を条件賦課するわけでもなく,複数分岐したすなわちリストではない tail や複数の head
のような,非常に奇妙なオブジェクトの存在をRDFグラフに書くこともできてしまう.
_:666 rdf:first <ex:aaa> .
_:666 rdf:first <ex:bbb>
.
_:666 rdf:rest <ex:ccc> .
_:666 rdf:rest rdf:nil .
rdf:rest プロパティの値の指定に失敗して,コレクションの定義不足であるトリプル集合を書いてしまう可能性もある.
そのようなグラフを排除するために,意味論的拡張として,この語彙の使用について特別の構文的な well-formedness な制約を置いてもよい.そのメンバーはrdf:firstの値の表示であるアイテムで表示されて,その順序はサブジェクトからrdf:nilへrdf:restプロパティを追跡することによって得られて,最後はrdf:nil
で終わるという,上記のような二つのトリプルのアイテムがリンクされたコレクションのサブジェクトが全順序列を表示するという約束事を破るようなコレクションの語彙の解釈を除いてもよい.これは別のシーケンスを含むシーケンスを可能にする.
RDFS 意味論条件により,後述のように,rdf:firstプロパティのサブジェクトと
rdf:restプロパティのサブジェクトとオブジェクトの型は,rdf:Listであるということに注意されたい.
3.3.4 rdf:value
rdf:value の使用の意図は,RDF Primer 文書[RDF-PRIMER
]で 直感的には説明されている.それは典型的にはいくつかの値を有する,あるいはいくつかのファセットすなわちそれ自身の属性を有する複雑なエンティティを値として有する,プロパティのうちの
'第1の' あるいは '主要な' 値を指定するために用いられる.
rdf:valueの有り得べき使用の範囲はとても広いので,意図された方法やユースケースのすべてをカバーする正確な記述を与えることは難しい.それゆえ,ユーザは
rdf:value
の意味はアプリケーションごとに異なることに注意されたい.実際に,意図された意味はしばしば文脈からは明らかであるが,グラフをマージしたり結論が推論されたときには失われてしまうかもしれない.
RDF スキーマ[RDF-VOCABULARY]
はより複雑な意味論的制約を有するより大きな語彙 rdfsV を含むように RDF を拡張する.
| RDFS 語彙 |
rdfs:domain rdfs:range rdfs:Resource
rdfs:Literal rdfs:Datatype rdfs:Class rdfs:subClassOf rdfs:subPropertyOf
rdfs:member rdfs:Container rdfs:ContainerMembershipProperty rdfs:comment
rdfs:seeAlso rdfs:isDefinedBy rdfs:label |
(rdfs:comment, rdfs:seeAlso,
rdfs:isDefinedBy そして rdfs:label はその使い方に適応される制約が
rdfs:domain, rdfs:range そして
rdfs:subPropertyOf を用いて述べられるので,ここに入れられている.)
厳密に必要と言うわけではないが,新しい意味論的構成である 'クラス'
を用いて RDFS 意味論を述べるのが便利である.すなわち,クラスとは,rdf:type
プロパティの値としてそのクラスがあるようなもののすべてである,ユニバース中の事物の集合を表現するリソースである.クラスは型
rdfs:Class の事物として定義され, ある解釈において,すべてのクラスの集合は IC
と呼ばれる.その意味論的条件は,IC から IR の部分集合の集合への ( I のクラス外延に対する ) 写像 ICEXT
を用いて述べられる.RDFS 語彙のrdf-解釈における
ICEXT と IC の意味は以下の RDFS 意味論的条件の表の最初の二つの条件で完全に定義される.あるクラスは空なクラス外延を有してもよいということ,(
先に述べたように
) 二つの異なるクラスエンティティが同一のクラス外延を有してもよいこと,rdfs:Class のクラス外延がクラス
rdfs:Class を含んでもよいこと,を注意しておく.
V の rdfs-解釈
とは,次の意味論的条件と RDFS の公理トリプル と呼ばれる引く続く表中のすべてのトリプルを充足するところの, (V union rdfV
union rdfsV)
の,ある rdf-解釈
I である.
RDFS 意味論的条件.
|
x ∈ ICEXT(y),iff 〈x,y〉∈
IEXT(I(rdf:type))
IC = ICEXT(I(rdfs:Class))
IR = ICEXT(I(rdfs:Resource))
LV = ICEXT(I(rdfs:Literal)) |
|
〈x,y〉∈
IEXT(I(rdfs:domain)) ∧〈u,v〉∈ IEXT(x) ⇒ u ∈ ICEXT(y) |
|
〈x,y〉∈
IEXT(I(rdfs:range)) ∧〈u,v〉∈ IEXT(x) ⇒ v ∈ ICEXT(y) |
|
IEXT(I(rdfs:subPropertyOf)) is
transitive and reflexive on IP |
|
〈x,y〉∈
IEXT(I(rdfs:subPropertyOf)) ⇒ x and y ∈ IP ∧ IEXT(x) ⊆
IEXT(y) |
|
x ∈ IC ⇒〈x,
I(rdfs:Resource)〉∈
IEXT(I(rdfs:subClassOf)) |
|
〈x,y〉∈
IEXT(I(rdfs:subClassOf)) ⇒ x and y ∈ IC ∧ ICEXT(x) ⊆
ICEXT(y) |
|
IEXT(I(rdfs:subClassOf)) is transitive
and reflexive on IC |
|
x ∈
ICEXT(I(rdfs:ContainerMembershipProperty)) ⇒
〈x,
I(rdfs:member)〉∈
IEXT(I(rdfs:subPropertyOf))
|
|
x ∈
ICEXT(I(rdfs:Datatype)) ⇒ 〈x,
I(rdfs:Literal)〉∈
IEXT(I(rdfs:subClassOf)) |
RDFS の公理トリプル.
rdf:type rdfs:domain rdfs:Resource
.
rdfs:domain rdfs:domain rdf:Property .
rdfs:range rdfs:domain
rdf:Property .
rdfs:subPropertyOf rdfs:domain rdf:Property .
rdfs:subClassOf
rdfs:domain rdfs:Class .
rdf:subject rdfs:domain rdf:Statement
.
rdf:predicate rdfs:domain rdf:Statement .
rdf:object rdfs:domain
rdf:Statement .
rdfs:member rdfs:domain rdfs:Resource .
rdf:first
rdfs:domain rdf:List .
rdf:rest rdfs:domain rdf:List .
rdfs:seeAlso
rdfs:domain rdfs:Resource .
rdfs:isDefinedBy rdfs:domain rdfs:Resource
.
rdfs:comment rdfs:domain rdfs:Resource .
rdfs:label rdfs:domain
rdfs:Resource .
rdf:value rdfs:domain rdfs:Resource .
rdf:type
rdfs:range rdfs:Class .
rdfs:domain rdfs:range rdfs:Class
.
rdfs:range rdfs:range rdfs:Class .
rdfs:subPropertyOf rdfs:range
rdf:Property .
rdfs:subClassOf rdfs:range rdfs:Class
.
rdf:subject rdfs:range rdfs:Resource .
rdf:predicate rdfs:range
rdfs:Resource .
rdf:object rdfs:range rdfs:Resource .
rdfs:member
rdfs:range rdfs:Resource .
rdf:first rdfs:range rdfs:Resource
.
rdf:rest rdfs:range rdf:List .
rdfs:seeAlso rdfs:range
rdfs:Resource .
rdfs:isDefinedBy rdfs:range rdfs:Resource
.
rdfs:comment rdfs:range rdfs:Literal .
rdfs:label rdfs:range
rdfs:Literal .
rdf:value rdfs:range rdfs:Resource .
rdf:Alt
rdfs:subClassOf rdfs:Container .
rdf:Bag rdfs:subClassOf rdfs:Container
.
rdf:Seq rdfs:subClassOf rdfs:Container
.
rdfs:ContainerMembershipProperty rdfs:subClassOf rdf:Property
.
rdfs:isDefinedBy rdfs:subPropertyOf rdfs:seeAlso
.
rdf:XMLLiteral rdf:type rdfs:Datatype .
rdf:XMLLiteral
rdfs:subClassOf rdfs:Literal .
rdfs:Datatype rdfs:subClassOf
rdfs:Class .
rdf:_1 rdf:type rdfs:ContainerMembershipProperty
.
rdf:_1 rdfs:domain rdfs:Resource .
rdf:_1 rdfs:range
rdfs:Resource .
rdf:_2 rdf:type
rdfs:ContainerMembershipProperty .
rdf:_2 rdfs:domain rdfs:Resource
.
rdf:_2 rdfs:range rdfs:Resource .
... |
I は rdf-解釈なので,
最初の条件は IP = ICEXT(I(rdf:Property)) ということを意味している.
これらの公理と条件には冗長性がいくらかある.例えば,ほとんどのRDF 公理トリプルが RDFS の公理トリプルと,ICEXTと,
rdfs:domain そして rdfs:range から導くことができる.すべての rdfs-解釈で真となるべきその他のトリプルは以下のとおり.
rdfs-valid なトリプル.
rdfs:Resource rdf:type rdfs:Class
.
rdfs:Class rdf:type rdfs:Class .
rdfs:Literal rdf:type rdfs:Class
.
rdf:XMLLiteral rdf:type rdfs:Class .
rdfs:Datatype rdf:type
rdfs:Class .
rdf:Seq rdf:type rdfs:Class .
rdf:Bag rdf:type
rdfs:Class .
rdf:Alt rdf:type rdfs:Class .
rdfs:Container rdf:type
rdfs:Class .
rdf:List rdf:type rdfs:Class
.
rdfs:ContainerMembershipProperty rdf:type rdfs:Class
.
rdf:Property rdf:type rdfs:Class .
rdf:Statement rdf:type
rdfs:Class .
rdfs:domain rdf:type rdf:Property .
rdfs:range
rdf:type rdf:Property .
rdfs:subPropertyOf rdf:type rdf:Property
.
rdfs:subClassOf rdf:type rdf:Property .
rdfs:member rdf:type
rdf:Property .
rdfs:seeAlso rdf:type rdf:Property .
rdfs:isDefinedBy
rdf:type rdf:Property .
rdfs:comment rdf:type rdf:Property
.
rdfs:label rdf:type rdf:Property
.
|
RDFS ではデータタイプはクラス外延を持つことができる,すなわちクラスと考えられていることに注意されたい.rdf:XMLLiteral
のクラス外延に関する意味論的条件によって示されるように,あるデータタイプクラスのメンバーはそのデータタイプの値である.このことは以下の第5節でより詳細に述べられる.ただし,クラスrdfs:Literalはすべてのリテラル値を含むが,その文字列が
datatypeの字句上の要求に従わない型付きリテラルについては,このクラスでの意味はない..
rdf-解釈の意味論的条件は
ICEXT(I(rdf:XMLLiteral))は well-typed なXMLリテラルのすべての
XML値を含むということを意味している.
rdf:XMLLiteralとrdfs:rangeを一緒にすると,プロパティ値はクラスrdf:XMLLiteralに所属しなければならないと述べても,そのプロパティ値が
ill-formed なXMLリテラルで,そのためそのクラスに所属しないという,条件によってはRDFSにおいて矛盾した宣言を書くこともできる.たとえば,
<ex:a> <ex:p> "<notLegalXML"^^rdf:XMLLiteral
.
<ex:p> rdfs:range rdf:XMLLiteral .
はrdfs-矛盾なので,いかなるrdfs解釈においても真ではない.
4.2 外延的意味条件 (情報提供)
上記の意味論はRDFS語彙の最も弱い'合理的な'解釈であるように慎重に選ばれている.意味論は値域,定義域,サブクラス,サブプロパティの意味論的条件を以下のような外延的な版に強化してもよい.
あるRDFS 意味論的条件のための外延的代替案.
|
<x,y> is in IEXT(I(rdfs:subClassOf)) if and only if
x and y are in IC and ICEXT(x) is a subset of ICEXT(y) |
|
<x,y> is in IEXT(I(rdfs:subPropertyOf)) if and only
if x and y are in IP and IEXT(x) is a subset of IEXT(y) |
|
<x,y> is in IEXT(I(rdfs:range)) if and only if (if
<u,v> is in IEXT(x) then v is in ICEXT(y)) |
|
<x,y> is in IEXT(I(rdfs:domain)) if and only if (if
<u,v> is in IEXT(x) then u is in ICEXT(y)) |
これはサブプロパティやサブクラスの性質が推移的かつ反射的であると保証するが,それ以上の結論ももたらす.
これらのより強い条件はプロパティがプロパティ外延に同一視され,クラスがクラス外延に同一視されるときに容易に充足されて,rdfs:subClassOfは部分集合の意味だと理解され,それゆえに
RDFSの外延的意味論によって充足される.何らかの方法で外延的な版はより簡単な意味論を提供するが,それにはより複雑な推論ルールが必要である.本文で記述される内包的意味論は,サブクラスとサブプロパティの宣言を最も一般的に使用するためのものであり,
7.3
節に記載されている RDFS 伴意ルールの 完全な集合のより簡単な実装を可能にする.
rdfs-解釈
に関する意味論的条件は, ICEXT(I(rdfs:Literal))は集合 LV
でなければならないという直感的には当然の条件を含むが,この条件を何らかのRDF宣言や推論ルールに重畳する方法は無い.この限界はリテラルがトリプルのサブジェクトの位置に現れることはできないためである.それでRDFにおけるリテラルについては,制限が厳しくてほとんど何も言うことができない.同様に,プロパティがクラスrdfs:Literalに関して述べられたとしても,それらが正しくリテラルそのものに転嫁されることはない.
例えば,次のトリプル
<ex:a> rdf:type rdfs:Literal .
はたとえ 'ex:a' がリテラルではなくURI参照であっても矛盾しない.それは I(ex:a)
がリテラル値である,すなわち,URI参照 'ex:a' がリテラル値を表示する
ということを述べるのであって,それがまさにリテラル値であると示すのではない.
意味論的条件は,プレーンリテラルのオブジェクトを含むいかなるトリプルも,オブジェクトとしてブランクノードを有する同様なトリプルを伴意することを保証する.
<ex:a> <ex:b> "10" .
は
<ex:a> <ex:b> _:xxx .
を伴意する.
これは,リテラルはエンティティを表示し,それゆえそのエンティティは,少なくとも原理的には,またURI参照による名前があってもよいという意味である.
4.4 RDFS 伴意
S のすべての要素を充足するどのrdfs-解釈も,また
E を充足するとき, S は E をrdfs-伴意する といい,S rdfs-entails E と書く.この言い方は, 第2節の単純伴意の定義に従うが,単純解釈のかわりにrdfs-解釈にだけ言及する.
rdfs-解釈は語彙伴意の一例である.
すべてのrdfs-解釈は,rdf-解釈なので,もし
S が E を rdfs-伴意するのなら,同時に
rdf-伴意するが,rdfs-伴意はrdf-伴意よりも強力である.数多くのrdfs-解釈が空グラフですら成り立つが,それにはrdf-解釈が成り立たないものがある.例えば,次の形式のすべてのトリプルは
xxx rdf:type rdfs:Resource .
URI参照 xxx を含むどんな語彙のrdfs-解釈においても真である.
しかしながら,あるrdfs-矛盾なグラフが伴意の定義からしてどんなグラフもrdfs-伴意するとしても,無矛盾な集合によるそのような'つまらない伴意'が,実際になにか有益な推論であるとは通常考えられない.
RDFは,特別のURI参照によって同定され,外部的に定義されたデータタイプのための機能を提供する.一般性を確保するために,RDFではデータタイプについて最小限の条件が重畳され,あるひとつの埋め込みのデータタイプrdf:XMLLiteralが含まれる.
ここでのデータタイプの意味論は最小であり,あるデータタイプをあるプロパティに関連させてそのプロパティのすべての値に応用するような準備は何も用意しない.また,ブランクノードが特定のデータタイプの値を表示するといったことを明示的に表明する方法を何も提供しない.
RDFは意味論的拡張により,将来はより精巧なデータタイプの条件を重畳してもよい.意味論的拡張はまたデータタイプについて,値空間の順序のような別種の情報を参照するかも知れない.
データタイプとは,
字句形式(lexical form) と呼ばれる文字列のある集合によって特徴付けられるエンティティであり,その集合から値(value)
への写像のことである.正確にこれらの集合と写像がどんな風に定義されるかは RDFのかかわらないところである.
形式的に,あるデータタイプ d は三つの事項で定義される.
1. d の字句空間 と呼ばれる文字列の空でない集合
2. d の値空間 と呼ばれる空でない集合
3. d の字句値写像 と呼ばれる,d の字句空間から d の値空間への写像
データタイプ d の字句値写像は L2V(d) と表記される.
その意味論を述べるにあたって,我々は解釈が,各データタイプがあるURI参照で同定されるところの特定のデータタイプ集合に関係づけられるものと仮定する.
形式的に,D は一つのURI参照と一つの データタイプ
からなるペアの集合としよう.その集合中にURI参照が2回は現れないとし,したがって D
はURI参照からデータタイプ集合への関数とみなすことができる.この関数をデータタイプ写像 と呼ぶ.
(特定のURI参照を明示的に述べて,その解釈がそのデータタイプ定義に対して責任のある外部の権威によって重畳される命名規則に従うこと確実にしなければならない.)
どのデータタイプ写像も
<rdf:XMLLiteral, x> を含むと理解される.ここで x
は埋め込みのXMLリテラルデータタイプであり,その字句空間と値空間と字句値写像はRDF Concepts and
Abstract Syntax 文書[RDF-CONCEPTS
]において 定義される.
データタイプ写像はまた形式
<http://www.w3.org/2001/XMLSchema#sss,
sss>であるすべてのペアの集合を含む.ここでsss は名前がXML Schema Part 2: Datatypes
[XML-SCHEMA2
]中にある sss である埋め込みのデータタイプであり,以下の表にリストされていて,ここではデータタイプ写像はXSDとして参照されている.
| XSD データタイプ |
xsd:string,
xsd:boolean,
xsd:decimal,
xsd:float,
xsd:double,
xsd:dateTime,
xsd:time,
xsd:date,
xsd:gYearMonth,
xsd:gYear,
xsd:gMonthDay,
xsd:gDay,
xsd:gMonth,
xsd:hexBinary,
xsd:base64Binary,
xsd:anyURI,
xsd:normalizedString,
xsd:token,
xsd:language,
xsd:NMTOKEN,
xsd:Name,
xsd:NCName,
xsd:integer,
xsd:nonPositiveInteger,
xsd:negativeInteger,
xsd:long,
xsd:int,
xsd:short,
xsd:byte,
xsd:nonNegativeInteger,
xsd:unsignedLong,
xsd:unsignedInt,
xsd:unsignedShort,
xsd:unsignedByte,
xsd:positiveInteger
|
そのほかの埋め込みXMLスキーマデータイプは,色々な理由で用いられる べきでない. xsd:duration
は well-defined
な値空間を持たないし(この点はXMLスキーマデータイプの改善によって後々訂正されるかも知れない.その場合には,改定されたデータタイプがRDFデータタイプ付けにおいて用いられることが適当かも知れない),
xsd:QName
と xsd:ENTITY
は XML文書を文脈に必要とする. xsd:ID
と xsd:IDREF
は XML文書中での相互参照のためのものであるし, xsd:NOTATION
は直接的な使用を目的とはしていない. xsd:IDREFS,
xsd:ENTITIES
と xsd:NMTOKENS
は順序付けのあるデータタイプでRDFデータタイプのモデルに合わない.
もし D がデータタイプ写像ならば,語彙
V のD-解釈 とは,D 中のすべてのペア< aaa, x >に対する以下の付加条件を充足する V union { aaa:D 中のある
x に対して< aaa, x >} のすべての解釈 I である.
データタイプに対する一般的意味論条件
| もし <aaa,x> が D の要素ならば,I(aaa) = x |
| もし <aaa,x> が D の要素ならば,ICEXT(x) は x の値空間でありかつ LV の部分集合 |
もし <aaa,x> が D の要素ならば, I(ddd) = x であるすべての V 中の型付きリテラル "sss"^^ddd
に対して,
もし sss が x の字句空間中の要素ならば, IL("sss"^^ddd) =
L2V(x)(sss), さもなければ IL("sss"^^ddd) は LV の要素ではない. |
もし <aaa,x> が D の要素ならば,I(aaa) は
ICEXT(I(rdfs:Datatype)) の要素 |
1番目の条件は I は提供されたデータタイプ写像
にしたがって,URI参照を解釈することを保証する.これは他のURI参照もそのデータタイプを参照することを妨げないということに注意されたい.
2番目の条件は,データタイプのURI参照がクラス名として用いられたときに, データタイプの値空間を参照し,かつある値空間のすべての要素はリテラル値でなければならないことを保証する.
3番目の条件は,語彙中の型付きリテラルがデータタイプの字句値写像に従うことを保証する.例えば,もし I がある XSD-解釈
ならば,I("15"^^xsd:decimal) は数15でなければならない. この条件はまた,ill-typed リテラル,すなわちリテラル文字列がデータタイプの字句空間中にはない場合,いかなるリテラル値も表示しないということでもある.直感的には,そのような名前はいかなる値も表示しないが,空な名前から起こる意味論的な複雑さを避けるためにそのような型付きリテラルは'代替の'非リテラル値を表示するとする.そうすると,例えば,もし
I がある XSD-解釈 だとして,I("arthur"^^xsd:decimal) で結論されるものは,まったく LV
中にはないということ,すなわち ICEXT( I(rdfs:Literal) ) 中にはないということである.ある ill-typed
な型付きリテラルはそれ自体では矛盾であることを構成しないけれども, ill-typed な型付きリテラルが rdf:type
rdfs:Literal と伴意するような,あるいは ill-typed なXMLリテラルが rdf:type
rdf:XMLLiteral と伴意するようなグラフは,矛盾することになる.
この3番目の条件は D の範囲でのデータタイプのみに限って適応されることに留意されたい.
その型が解釈のデータタイプ写像にない型付きリテラルについては,以前のように,すなわち,何か未知なものを表示するように扱われる.この条件はその型付きリテラル中のURI参照がデータタイプの関連URI参照と同じのはずであるということを要求しない.これによって適切な結論を導くような,URI参照についての同定条件を表現する意味論的な拡張が可能となる.
4番目の条件は,クラスrdfs:Datatypeが,いかなる充足的D-解釈においても用いられる
データタイプを含むことを保証する.これは必要ではあるが十分ではないことに留意されたい.クラス
I(rdfs:Datatype) は別のデータタイプを含むことができる.
rdf-解釈のための意味論的条件は
'rdf:XMLLiteral'によって型付けされるリテラルに正しい解釈を重ねる.しかしながら,D-解釈ではRDF型付きリテラルの構文論に単純に意味論的条件を重ねるのではなく,
データタイプがエンティティとして存在することを認める.それゆえ,D-解釈からrdfs-解釈よりも強力な結論を導く.
もしデータタイプ写像においてデータタイプがその値空間上に互いに素(disjointness)条件を重ねるのなら,RDFグラフにそれを充足するD-解釈がないということが有り得る.例えば,XMLスキーマではxsd:stringとxsd:decimalの値空間は互いに素であるので,グラフ
<ex:a> <ex:b> "25"^^xsd:decimal .
<ex:b>
rdfs:range xsd:string .
を充足する XSD-解釈を構成できない.
この状況はグラフのXSD-矛盾,あるいはより一般的にデータタイプクラッシュ と言われている.このグラフで充足的なrdfs-解釈を構成することは可能なのだが,
I(xsd:decimal) と I(xsd:string) のクラス外延の共通集合は空なので,それは
XSD 条件に違反するのである.
データタイプクラッシュは他のいくつかの方法でも起こり得る.例えば,何かが互いに素なデータタイプクラスの両方に属すると表明したり,
_:x rdf:type xsd:string .
_:x rdf:type xsd:decimal .
有り得ない値域を有するプロパティが値を持ったり
<ex:p> rdfs:range xsd:string .
<ex:p> rdfs:range
xsd:decimal .
_:x <ex:p> _:y .
するとデータタイプクラッシュとなる.データタイプクラッシュは特定の字句形式の使用からも起こりえる.例えば,
<ex:a> <ex:p> "2.5"^^xsd:decimal .
<ex:p>
rdfs:range xsd:integer .
はデータタイプクラッシュであり,あるいは ill-typed な字句形式の使用
<ex:a> <ex:p> "abc"^^xsd:integer .
<ex:p>
rdfs:range xsd:integer .
もデータタイプクラッシュとなる.
データタイプクラッシュはこのモデル理論によってのみ矛盾と認知されるけれども,
XMLリテラルを巻き込むことでRDFSにおいてデータタイプクラッシュが起こりえるということを注意しておく.
もし D が D' の部分集合ならば,D'-解釈へグラフの解釈を制限することで,D
に関しても同様な制約の意味論的拡張を得ることとなる.実際,データタイプ写像の拡張は,型付きリテラルが
データタイプの値空間におけるエンティティを表示することを要求することによって,型付きリテラルについて暗黙の表明をすることである.より大きなデータタイプ写像に関連した付加的意味論条件は解釈がより多くのトリプルを真にすることを強制するが,しかしまたデータタイプクラッシュと違反も明らかにして,
D-整合グラフがD'-矛盾であるようにもなる.
あるRDFグラフが形式
aaa rdf:type rdfs:Datatype .
のデータタイプトリプル を rdfs-伴意するとき,そのグラフはデータタイプURI参照 aaa を認知する
という.
rdfs-解釈のための意味論的条件によって埋め込みのデータタイプURI参照
'rdf:XMLLiteral' が認知される.
もしあるグラフ中のすべての認知されたURI参照が,分かっているデータタイプの名前ならば,そのとき個々の認知されたURI参照からその分かっているデータタイプへのペアを作る(そして'rdf:XMLLiteral'
からrdf:XMLLiteralへの),自然なデータタイプ写像
DG がある.そのとき,そのグラフのいかなるrdfs-解釈
I も I(aaa) が適切なデータタイプでありかつrdfs:Datatypeのクラス外延が正しく修正されていることを除けば
I であるかのような,相当する'自然な'DG-解釈を有する.アプリケーションは D がグラフの自然なデータタイプ写像を含むようなD-解釈によって解釈されることを要求
してもよい.そしてデータタイプトリプルをグラフによるデータタイプ'宣言'として扱うことになり,4番目の意味論的条件は必要十分条件('iff')となる.しかしながら,データタイプトリプルは,それ自体ではあるグラフがその他のデータタイプの意味論的条件を充足するかどうかチェックするのに必要な情報を提供しはしないし,形式的にはその他の解釈を導出しないので,形式的な伴意の原則としてこの要求を採用することは,以下の第6節で述べる一般単調性レンマを破ることになる.
5.2 D-伴意
S のどの要素も充足するすべてのD-解釈が,E
もまた充足するとき,S は E をD-伴意する という.この言い方は第2節の単純伴意にならったものであるが,すべての単純解釈ではなく,D-解釈のみに限ったことである.
D-解釈は語彙解釈の一例である.
上に注記したように,あるグラフがある語彙において無矛盾であっても,より大きな語彙について定義された意味論的拡張において矛盾することはありえるし,D-解釈があるRDFグラフにおいて矛盾を許容することもできる.
語彙伴意の定義が意味するところは,矛盾するグラフはより強力な語彙伴意においていかなる
グラフでも伴意するであろうということである.例えば,ある D-矛盾なグラフはいかなるRDFグラフでもD-伴意する.しかし,それらはより小さな語彙では正しい伴意ではないかも知れないので,そのような'あたりまえの'伴意を有益な結論と考えることは通常適切ではないだろう.
6. 意味論的拡張の単調性
RDFグラフのある集合が与えられて,それに情報を'追加する'には様々な方法がある.どんなグラフでもそれに追加されるトリプルが有り得て,そのグラフ集合は追加のグラフによって拡張され得る.あるいは,グラフの語彙は語彙伴意のより強力な概念に関して解釈され得る.すなわち,意味論的条件のよりおおきな集合で解釈において重ねあわされるものと理解される.これらのすべては情報の追加と考えられており,変化の前に成立していたよりも多くの伴意を作り出すことができる.これらすべての追加は,情報が加わる前に成立していた伴意は,その後も成立するという意味において,
単調である.これを次の一つのレンマでまとめることができる.
一般単調性レンマ. S と S' を S のすべてのメンバーが S'
のいずれかのメンバーであるようなRDFグラフの集合であるとする.Y は X の意味論的拡張を表し,S は E を X-伴意して, S と E は Y
のいかなる構文論的制約も充足するものとする.そのとき,S' は E を Y-伴意する.
特に,もし D' がデータタイプ写像のときは,D'
の部分集合 D で,もし S が E をD-伴意するのなら,S
もまた E を D'-伴意する.
7. 伴意ルール(情報提供)
以下の表では,語彙伴意の様々な形式のうちのいくつかについて,
RDFとRDFS伴意のためにRDFSグラフをチェックするソフトウェア設計のガイドとして用いることのできる推論パターンをリストする.実装はルールを前向きに応用することをベースとするが,提出された伴意の帰結部に認められる一つのパターンを結論として,提出された前件部に正しくマッチする他のルールの結論をもとめて後向きに探索してもよい.
ルールはすべて あるグラフがあるパターンに一致するトリプルを含むとき,あるトリプルがグラフに追加される
という形式で述べられる.そしてそれらはすべて,正当に,あるグラフが,元々のグラフにルールを適応することによって得られる,よりおおきなグラフを(リストされた適切な意味において)伴意する,あるグラフにルールを適応することで,マージではなく,結論の単純な合併を形成することを注意しておく.そのゆえに,グラフ中にすでにあるどんなブランクノードも保存される.
これらのルールは次のような規約で用いられる.aaa,bbb,等はトリプル中の任意の可能なプレディケイトであるURI参照を表す.uuu,vvv,等は,トリプル中の任意の可能なサブジェクトである,URI参照あるいはブランクノード識別子を表す.
xxx,yyy,等はトリプル中の任意の可能なサブジェクトあるいはオブジェクトである,URI参照あるいはブランクノード識別子あるいはリテラルを表す.lll
はリテラルを表し,_:nnn 等はブランクノード識別子である.
7.1 単純伴意ルール
第2節の内挿レンマは,汎化グラフすなわち元のグラフをインスタンスとするグラフを生成する以下の伴意ルールにより,特徴付けられる.サブグラフとすることに,トリプルに関する推論ルールとして明示的な形式化は必要ない.
単純伴意ルール
| Rule name |
If E contains |
then add |
| se1 |
uuu aaa xxx . |
uuu aaa _:nnn . ここで _:nnn は
ルール se1 あるいは se2 によって xxx にアロケイトされるブランクノードの識別子. |
| se2 |
uuu aaa xxx . |
_:nnn aaa xxx .
ここで _:nnn は
ルール se1 あるいは se2 によって uuu にアロケイトされるブランクノードの識別子. |
用語 'アロケイトされる'
とは,ブランクノードが同じURI参照,ブランクノードあるいはリテラルに関して,この明示されたルールを適用することにより,先に作られていなければならないということを意味している.すなわち,もしそのような該当するブランクノードがなければ,グラフ中にはなかった
'新しい'
ノードが作られなければならない.この少しややこしい条件は,新しいブランクノードのトリプルを追加することで得られるグラフが元のグラフを正規なインスタンスとすることを確実にし,そのようなグラフであればどんなものでも,これらのルールによって生成されるものとして同じサブグラフを有するようになることを保証する.例えば,次のグラフ
<ex:a> <ex:p> <ex:b> .
<ex:c> <ex:q>
<ex:a> .
は次のように拡張されてよい.
_:x <ex:p> <ex:b> . ex:aにアロケイトされる新しい_:xを用いる
se1 によって
<ex:c> <ex:q> _:x .
ex:aにアロケイトされる同じ_:x を用いる se2 によって
_:x
<ex:p> _:y . ex:bにアロケイトされる新しい_:yを用いる
se2 によって
しかし,次のように推論することは正しくない.
** _:x <ex:q> <ex:a> . ** se2 によって(**
_:x は ex:c にはアロケイトされていないので)
これらのルールはブランクノードを急激に増やして,非常に非簡約なグラフを生成することを可能にする.次のような伴意が容認される.
<ex:a> <ex:p> <ex:b> .
<ex:a>
<ex:p> _:x . ex:b にアロケイトされる
_:x を用いた xse1 によって
<ex:a> <ex:p> _:y . _:x にアロケイトされる
_:y を用いた xse1 によって
_:z <ex:p> _:y . ex:a にアロケイトされる
_:z を用いた xse2 によって
_:u <ex:p> _:y . _:z にアロケイトされる
_:u を用いた xse2 によって
_:u <ex:p> _:v . _:y にアロケイトされる
_:v を用いた xse1 によって
もしこれらのルールを適切な順序で適応することにより,S から E が導かれるならば,そしてそのときにのみ S は E
のインスタンスであることは,容易に分かる.それで,内挿レンマにより,これらのルールの適応によって S から E (を含むグラフ)が導かれるとき,そのときのみ,S
は単純に E
を伴意する.しかし,ルールは停止することなく等価なトリプルの多くの冗長な結果を導くことができるので,ただ素朴にこれらのルールを適応しても,有効な探索プロセスにはならないということもまた,明らかである.
任意のRDFグラフ間の単純伴意を決定するという一般的問題は,決定可能(decideable)ではあるが
NP-完全である.このことは,グラフを表現するブランクノードのみを用いて(Jeremy Carrollによる観察)
RDF伴意として任意の有向グラフのサブグラフを取り出すという問題をコード化することによって,示される.
RDFとRDFS伴意検出のための次のルール集合は,ルール se1 をリテラルに適用した特殊なケースである.
リテラル汎化ルール
| Rule Name |
If E contains |
then add |
| lg |
uuu aaa lll . |
uuu aaa _:nnn . ここで _:nnn
はこのルールによってリテラル lll にアロケイトされるブランクノードの識別子である. |
このルールは,一つのリテラルが与えられて,そのリテラルを含むすべてのトリプルからなる E
のどんなサブグラフでも,そのリテラルがユニークなブランクノードによって置き換えられた同型のサブグラフとして再生成するのに十分であることに注意されたい.これの顕著な特徴は,RDFトリプルにおいてサブジェクトの位置にブランクノードがくることができて,そのリテラルによって表示されるリテラル値の性質を表現する他のルールによって,結論を導くことができるというところにある.
RDFS伴意に対してはルール lg に反対の追加ルールが必要である.
リテラルのインスタンシエーションルール
| Rule Name |
If E contains |
then add |
| gl |
uuu aaa _:nnn .
ここで _:nnn はルール
lgによって,リテラル lll に アロケイトされるブランクノードの識別子である. |
uuu aaa lll . |
あきらかに,アロケイトされたブランクノードが他の推論ルールによって新しいトリプルのオブジェクトの位置に導入される場合以外ではルール gl
は単純に冗長さを生み出すだろう.これらのルールの効果はリテラルを含むどんなトリプルでも,アロケイトされたブランクノードを含む類似のトリプルと互いに導出が可能であるというところにあり,リテラルはこれらのルールを適用することを目的にアロケイトされたブランクノードで識別することができる.
7.2 RDF 伴意ルール
RDF 伴意ルール
| Rule Name |
if E contains |
then add |
| rdf1 |
uuu aaa yyy . |
aaa rdf:type rdf:Property . |
| rdf2 |
uuu aaa lll . ここで lll は well-typed なXMLリテラル. |
_:nnn rdf:type rdf:XMLLiteral .
ここで _:nnn はルール
lg によってアロケイトされるブランクノードの識別子. |
これらのルールは,次の意味で完全
である.
RDF 伴意レンマ.もしルール
lg とRDF
伴意ルールの適用によって, S に加えてRDF
公理トリプルから引き出されるグラフがあって,それが E を単純に伴意するならば,そしてそのときのみ,
S は E をrdf-伴意する.
(証明は
付録 A)
これはルール
glを使用する必要がないことを注意しておく.
7.3 RDFS 伴意ルール
RDFS 伴意ルール.
| Rule Name |
If E contains: |
then add: |
| rdfs1 |
uuu aaa lll.
ここで lll はプレーンリテラル(言語タグ有りあるいは無し). |
_:nnn rdf:type rdfs:Literal .
ここで _:nnn はルール
lg によって lll にアロケイトされるブランクノード識別子. |
| rdfs2 |
aaa rdfs:domain xxx .
uuu aaa yyy
. |
uuu rdf:type xxx . |
| rdfs3 |
aaa rdfs:range xxx .
uuu aaa vvv
. |
vvv rdf:type xxx . |
| rdfs4a |
uuu aaa xxx . |
uuu rdf:type rdfs:Resource . |
| rdfs4b |
uuu aaa vvv. |
vvv rdf:type rdfs:Resource . |
| rdfs5 |
uuu rdfs:subPropertyOf vvv .
vvv
rdfs:subPropertyOf xxx . |
uuu rdfs:subPropertyOf xxx . |
| rdfs6 |
uuu rdf:type rdf:Property . |
uuu rdfs:subPropertyOf uuu . |
| rdfs7 |
aaa rdfs:subPropertyOf bbb .
uuu aaa yyy
. |
uuu bbb yyy . |
| rdfs8 |
uuu rdf:type rdfs:Class . |
uuu rdfs:subClassOf rdfs:Resource . |
| rdfs9 |
uuu rdfs:subClassOf xxx .
vvv
rdf:type uuu . |
vvv rdf:type xxx . |
| rdfs10 |
uuu rdf:type rdfs:Class . |
uuu rdfs:subClassOf uuu . |
| rdfs11 |
uuu rdfs:subClassOf vvv .
vvv
rdfs:subClassOf xxx . |
uuu rdfs:subClassOf xxx . |
| rdfs12 |
uuu rdf:type rdfs:ContainerMembershipProperty . |
uuu rdfs:subPropertyOf rdfs:member . |
| rdfs13 |
uuu rdf:type rdfs:Datatype . |
uuu rdfs:subClassOf rdfs:Literal . |
これらのルールに対する完全性を述べるには,
ill-typed なXMLリテラルについて非充足な表明を含むために グラフがrdfs-矛盾となる可能性があるので,注意が必要である.例えば,
<ex:a> rdfs:subClassOf rdfs:Literal
.
<ex:b> rdfs:range <ex:a>
.
<ex:c> rdfs:subPropertyOf
<ex:b>.
<ex:d> <ex:c> "<"^^rdf:XMLLiteral
.
ここで ill-typed なXMLリテラルの表示はリテラル値を必要としないが,他の表明に基づいて推論されることはあり得る.そのような
rdfs-矛盾なグラフは,仮に構文論的には関係ない前件部だとしてもすべての RDF グラフを
rdfs-伴意するので,そのような場合を除かなければならない.
次の形式のトリプルを導くことで,伴意ルールによって矛盾を認識できるという特徴的なシグナルがある.
xxx rdf:type rdfs:Literal .
ここで xxx はルール
lgによって, ill-typed なXMLリテラルにアロケイトされる.そのようなトリプルをXML
clash と呼ぶ.上記例では,そのようなクラッシュが素直に導かれる.
<ex:d> <ex:c> _:1 . (ルール
lg によって,_:1 は "<"^^rdf:XMLLiteralにアロケイトされる)
<ex:d>
<ex:b> _:1 . (ルールrdfs7
によって)
_:1 rdf:type <ex:a>. (ルールrdfs3によって)
_:1
rdf:type rdfs:Literal . (ルールrdfs9によって)
そのとき,これらのルールは次の意味で,完全である.
RDFS 伴意レンマ.もしルール
lg,ルール
gl と RDF
および RDFS
伴意ルールの適用によって, S に加えてRDF
および RDFS
公理トリプルから導くことのできるグラフがあって,それが E を単純伴意するか,あるいは
XML クラッシュを含むのなら,そしてそのときにのみ,S は E をrdfs-伴意する.
(証明は
付録 A にある)
RDFS ルールには冗長性がある.例えば,RDF
公理トリプルのそのほとんどすべてが,ルールrdfs2
および rdfs3
と RDFS
公理トリプルから導くことができる.
これらのルールの出力はしばしば他のルールをトリガーする.これらのルールはグラフ中のすべてのrdf:type表明についてすべてのスーパープロパティやスーパークラスに対して,それを再表明しながら,そのサブプロパティ階層やサブクラス階層の上位に伝播させる.
rdf1
はグラフ中に用いられるすべてのプロパティ名に対してタイプ表明を生成するし,rdfs3
は最新の RDFS
公理トリプルと共に,用いられているすべてのクラス名に対してすべてのタイプ表明を追加する.いかなるサブプロパティやサブクラス表明も,rdfs2
や rdfs3
や RDFS 公理トリプル集合中の定義域表明と値域表明によって適切なタイプ表明を生成する.語彙 V 中のすべての uuu について
uuu rdf:type rdfs:Resource .
が生成され,すべてのクラス名 uuu について
uuu rdfs:subClassOf rdfs:Resource .
が生成される.そして次のような,いくつかのより '普遍的' な事実
rdf:Property rdf:type rdfs:Class .
も生成される.
7.3.1 外延的伴意ルール
第
4.1 節に記載されたより強力な外延的意味論条件は, RDFS
ルールではカバーされないさらなる伴意を是認する.以下の表ではこのより強力な意味論において正しい伴意パターンのいくつかがリストされている.これは外延的意味論条件に対する完全なルール集合ではない.これらのルールのいずれもrdfs-正当ではなく,第
4.1
節記載の強化された外延的意味論条件に適応されるところの,意味論的外延にのみあてはまるものであることを注意しておく.これらのルールはその他の結論ももたらす.例えば,
rdfs:Resourceはすべてのプロパティの定義域と値域である.
ルール ext5-ext9 は共通のパターンにしたがうが,それらは強化された外延的条件には,可能なかぎり大きな rdfV と rdfsV
の語彙において,プロパティの定義域(そして推移的なプロパティに対する値域)が必要であるという事実の反映である.そのため,これらを制限しようとしてもその試みは,意味論的条件によってひっくりかえされてしまうだろう.同様なルールが
rdfs:range と rdfs:domain
のスーパープロパティにも適応されるが,実際にそのようなケースは起こることはありそうも無い.
RDFS 意味論的条件の外延的改訂版において正当となる追加的推論のいくつか.
| ext1 |
uuu rdfs:domain vvv .
vvv
rdfs:subClassOf zzz . |
uuu rdfs:domain zzz . |
| ext2 |
uuu rdfs:range vvv .
vvv
rdfs:subClassOf zzz . |
uuu rdfs:range zzz . |
| ext3 |
uuu rdfs:domain vvv .
www
rdfs:subPropertyOf uuu . |
www rdfs:domain vvv . |
| ext4 |
uuu rdfs:range vvv .
www
rdfs:subPropertyOf uuu . |
www rdfs:range vvv . |
| ext5 |
rdf:type rdfs:subPropertyOf www
.
www rdfs:domain vvv .
|
rdfs:Resource rdfs:subClassOf vvv
. |
| ext6 |
rdfs:subClassOf
rdfs:subPropertyOf www .
www
rdfs:domain vvv .
|
rdfs:Class rdfs:subClassOf vvv
. |
| ext7 |
rdfs:subPropertyOf rdfs:subPropertyOf
www .
www rdfs:domain vvv .
|
rdf:Property rdfs:subClassOf vvv
. |
| ext8 |
rdfs:subClassOf
rdfs:subPropertyOf www .
www
rdfs:range vvv .
|
rdfs:Class rdfs:subClassOf vvv
. |
| ext9 |
rdfs:subPropertyOf rdfs:subPropertyOf
www .
www rdfs:range vvv .
|
rdf:Property rdfs:subClassOf vvv
. |
7.4 データタイプ伴意ルール
データタイプ伴意を表明と伴意ルールの見地から捉えるには,
データタイプ自体によって提供される情報に言及し,
データタイプのおおもとを調べることでチェックするしかないような構文論的条件を仮定するのに必要なルールを述べる必要がある.
データタイプについて利用可能な各種情報に対して,その種の情報向きの推論ルールを述べることができるが,それはRDFS
伴意ルール表の拡張と考えられる.これらは埋め込みデータタイプ以外のデータタイプへの応用と考えられるべきであり,
RDFS 伴意ルールの一部に対するルールである.以下に述べるルールでは,認められたURI参照によって表示される データタイプについて利用可能な情報があるものと仮定しており,そのデータタイプに言及する
URI参照を用いている.
各リテラル文字列に対して,基本的な情報として,それがデータタイプの正しい字句形式であるかないかを特定する.すなわち,そのデータタイプの字句値写像においてある値に写像されるものを特定する.それは
ddd により表示されるデータタイプに対する正しい字句形式である各文字列
sss についての,次のルールに相当する.
| rdfD1 |
ddd rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd
. |
_:nnn rdf:type ddd .
ここで _:nnn はルール
lgによって "sss"^^ddd に アロケイトされるブランクノードの識別子である. |
二つの字句形式 sss と ttt が ddd によって表示されるデータタイプの下で,同じ値に写像されるものとしよう.そのとき次のルールが適応される.
| rdfD2 |
ddd rdf:type rdfs:Datatype .
uuu aaa "sss"^^ddd
.
|
uuu aaa "ttt"^^ddd . |
ddd で表示されるデータタイプの字句形式
sss と eee で表示されるデータタイプの字句形式
ttt が同じ値に写像されるものとしよう.そのとき次のルールが適応される.
| rdfD3 |
ddd rdf:type rdfs:Datatype .
eee rdf:type
rdfs:Datatype .
uuu aaa "sss"^^ddd .
|
uuu aaa "ttt"^^eee . |
加えるに,もし ddd の表示するデータタイプの値空間が,
eee の表示するデータタイプの値空間の部分集合であると分かっていれば,
ddd rdfs:subClassOf eee .
と表明することは適切である.
しかし,これは部分集合関係からだけでは得られないので,明示的に表明される必要がある.
これらのルールにおいてコード化された情報は正しいものと仮定して,これらとそれ以前のルールを適応することで得られるグラフはオリジナルによってD-伴意されたグラフである.
ルール rdfD2 と 3
は基本的に字句形式間の等価性による代入である.そのような等式は無限の多くの結論を生成する能力がある.例えば,正しいxsd:integerの字句形式であることを止めることなく,頭にゼロをいくつでもつけることができる.そのような正しくはあるが,救いようの無い推論を避けるためには,基準となる形式があるときには,問題のデータタイプについてそのような基準形式で字句形式を置き換えるように
rdfD2
を制限するだけで十分である.しかしながら,正しい伴意を省略することのないように,そのような基準化ルールは提案された伴意の前件部と同じく結論にも適応されるべきであるし,
rdfD3 タイプと同じルールは個々のデータタイプの基準形式の間で同定のための知識を反映する必要があるだろう.
特別な場合には,他の情報も利用可能かも知れず,特定の RDFS
語彙を用いることができるかも知れない.そのようなデータタイプ固有の意味がさらに意味論的拡張によって定義されてもよい.
これらのルールは,認められたデータタイプのどんな well-formed
な型付きリテラルも,クラスrdfs:Literalにおける何かを表示すると結論することができる.
<ex:a> <ex:p> "sss"^^<ex:dtype> .
<ex:dtype>
rdf:type rdfs:Datatype .
<ex:a> <ex:p> _:nnn . (ルール
lg によって)
_:nnn rdf:type <ex:dtype> .
<ex:dtype> rdfs:subClassOf rdfs:Literal .
_:nnn rdf:type rdfs:Literal .
ルール rdfD1 は以下の式の推論連鎖によってデータタイプクラッシュのいくつかのケースにつき,それを暴露することができる.
<ex:p> rdfs:range <ex:dtype> .
<ex:a> <ex:p>
"sss"^^<ex:otherdtype> .
<ex:a> <ex:p> _:nnn .
_:nnn rdf:type
<ex:otherdtype> . (ルール rdfD1
によって)
_:nnn rdf:type <ex:dtype> . (ルール rdfs3
によって)
特定のデータタイプのための正しいD-伴意は,特定のデータタイプの特有の性質に依存するので,これらのルールは値空間のサイズのように
D-伴意の推論法則の完全な集合を提供しない. (例えば xsd:boolean
は二つの要素しかなく,二つの値に対して確立されたどんなものでも,このデータタイプを有するすべてのリテラルに対して真とならなければならない.) 特に,XSD データタイプであるxsd:string
の値空間と字句値写像では,言語タグなしのプレーンリテラルと型付きリテラルの両方が,そのリテラル中に表示された (displayed) ユニコード文字列を表示する
(denote) ので,データタイプの字句空間におけるすべての文字列に対して両者は同一とする.それで,以下の推論ルールはすべての
XSD-解釈において正しい.ここで,'sss' はxsd:stringの字句空間における任意の
RDF 文字列である.
| xsd 1a |
uuu aaa "sss". |
uuu aaa "sss"^^xsd:string . |
| xsd 1b |
uuu aaa "sss"^^xsd:string . |
uuu aaa "sss". |
ルール rdfD2 や rdfD3
を用いるのと同様に,アプリケーションはこれらのルールを直接適用するのではなく,これらの等価な形式の一つを他の一つと系統的に置き換えをしてもよい.
"証明の利点の一つは,証明された結果について確かな疑問を抱かせることである." -Bertrand Russell
空グラフのレンマ.
トリプルの空集合はどんなグラフによっても伴意されるが,それは自分自身を除くどんなグラフも伴意しない.
証明. N をトリプルの空集合としよう.グラフに関する意味論的条件は いかなる I に対しても,N が I
において真であることを要求する.したがって,一番目の部分は伴意の定義から得られる. G を任意の空でないグラフとし,s p o
.を G 中のあるトリプルとする.そのとき,IEXT(I(p)) = { } を有する 解釈 I は N を充足するが G
は充足しない.したがって N は G を伴意しない.QED.
これは,以下に続く結果のほとんどは空グラフに対しては当然であり,予期されることであることを意味している.
サブグラフのレンマ.
グラフはそのサブグラフすべてを伴意する.
証明. サブグラフ
と 伴意の定義から自明である.もしグラフが
I において真でそのときある A に対して真であれば,そのトリプルすべては I+A において真である. したがって,トリプルのすべての部分集合は I
において真である.QED
マージのレンマ. RDFグラフ集合 S
のマージは
S によって伴意され,S のすべてのメンバーを伴意する.
証明. 伴意とマージの定義から自明.
S のすべてのメンバーは,もしS のマージ中のすべてのトリプルが真であるときそのときのみ真である.
QED.
これは,本文中で述べたように,グラフのある集合は充足性と伴意を議論するときに,あたかも単一のグラフであるかのように扱うことができるということを意味している.この約束事は以下の
付録
において採用され,あるグラフ集合,あるグラフを伴意するグラフ集合,等々の解釈への言及は,どの場合もグラフ集合のマージへの言及として理解されなければならず,以下において
'グラフ' と言ったときには,それはグラフやグラフの集合を言っているものとされる.
インスタンスのレンマ.
グラフはそのすべてのインスタンスによって伴意される.
証明. I は E' を充足し,E'
は E のインスタンスと仮定する.
そのとき,E' のブランクノードに関するある写像 A に対して,I+A は E' におけるすべてのトリプルを充足する. E 中の各ブランクノード b
に対して,B(b)=I+A(c) を定義する.ここで c はブランクノードあるいは E' 中の b に置き換わる名前であるか,
あるいはもし置き換わるものがなければ,c=b である.そのとき,I+B(E)=I+A(E')=true であり,したがって I は E を充足する.しかし
I は任意であった.したがって E' は E を 伴意する.
QED.
スコレム化とは,自動推論システムにおいてルーチン的に用いられる構文論的変換であり,存在変数が - どこにも用いられていない
- '新しい' 関数によって置き換えられ,全称変数は閉包される.RDF
においては,スコレム化とは,グラフ中のすべてのブランクノードを名前で,すなわちそれまでどこにも現れていないことが保障されているURI参照で,置き換えることである.実際上,それはブランクノードを使用することで表明されていた,匿名のエンティティの存在にたいして,
'任意的な'
名前を与える.名前の任意性が,ブランクノードによってあらわされる存在のありのままの表明からは推論されるものが何も無いということを保障する.(リテラルを使うとそうはならない.リテラルは要求された意味では決して
'新しく' はない.)
厳密に言えば,(V に関する) E の スコレム化 は,1:1 のインスタンス写像を有する,V に関する E
の基底インスタンスであって, G 中の各ブランクノードが G 中には現れないURI参照に写像される.(したがって,スコレム語彙 V は E
の語彙とは互いに素(disjoint)でなければならない.)
スコレム化は,それ自体では厳密な意味では正しい(valid)操作ではないけれども,スコレム化された表現はスコレム語彙のない元の表現と同じ伴意を有しているという意味において,表現に何も新しい内容を付け加えない.
スコレム化のレンマ. sk(E) を V
に関する E のスコレム化とする.すると sk(E) は E を伴意する.そして,もし sk(E) が F を伴意して,F の語彙が V
と互いに素(disjoint)ならば, E は F を伴意する.
証明. インスタンスのレンマにより sk(E) は E を伴意する.
さて,sk(E) は F を伴意するとしよう.ここで F は V と語彙を共有しない.そして I は E を充足するある解釈であるとする.そのとき,E
のブランクノードからのある写像 A に対して, I+A は E を充足する.sk(E) の語彙の解釈 I' を,IR'=IR,IEXT'=IEXT,E
の語彙中の x に対して I'(x)=I(x), V 中の x に対しては I'(x)=[I+A](y) とする.ここで y は sk(E) における x
によって置き換えられる E 中のブランクノードである. 明らかに,I' は sk(E) を充足する.したがって,I' は F を充足する.しかし F
の語彙は V の語彙とは互いに素であるので, I'(F)=[I+A](F) である.しかし,I は任意であり,したがって E は F を伴意する.
QED.
直感的には,このレンマはスコレム化は,多くの点で,元のグラフの表明と類似の内容を表現することを示している.しかしながら,これらの '任意の'
名前は一旦発行されるとその他のURI参照と同じ状態となるので,グラフはそのスコレム化と等価であると考えられるべきではない.また,スコレム化は伴意の前件部以外のものに適応されたときには適切ではない操作となる.クエリのスコレム化は完全に異なるクエリをあらわすだろう.それにもかかわらず,伴意について結果を証明するときに多くの目的のために,我々は基底グラフを考えるだけでよい.スコレム語彙を含まない
E が供給されると, S は,もし S' が E を伴意するときそしてそのときのみ E を伴意する.
以下のレンマの証明では,グラフ自身における字句要素を用いることによってグラフの解釈を構成するやりかたを採用する. (これはエルブランの考えであった.我々はここではそれをちょっと変更して,リテラルを適切に取り扱う.)
空でないグラフ G が与えられて,G の いわゆる(単純)エルブラン解釈 とは,Herb(G) と書いて,以下に定義される解釈である.
|
LVHerb(G) = G 中のすべてのプレーンリテラルの集合;
IRHerb(G) = G 中のトリプルのサブジェクトとオブジェクトの位置に現れる 名前とブランクノードの集合;
IPHerb(G) = G 中のトリプルのプロパティの位置に現れるURI参照の集合;
IEXTHerb(G) = {<s,o>: G が含むトリプル s p o . }
ISHerb(G) と ILHerb(G) は両方とも G
の語彙の適切な部分上への同定写像である. |
明らかに Herb(G)+B は,ここで B は G 中のブランクノードへの同定写像,構成されて G
中のすべてのトリプルを充足する.したがって,Herb(G) は G を充足する.
エルブラン解釈は
URI参照と型付きリテラル (とブランクノード) を,プレーンリテラルと同様に,すなわち,それ固有の構文的形式を表示するかのごとく,取り扱う.もちろんこれは
RDF の書き手によって意図されたことではないが,それはどんなグラフのこのように解釈 可能である
ことを示している.それゆえ,このことはいかなるRDFグラフも充足する単純解釈を有すること,すなわち
RDF において単純に矛盾するものではないことを立証する.
G のエルブラン解釈のユニバースは G のブランクノードを含むことに注意されたい.それらは,実際,その存在を表明するエンティティを '代表'
する.ブランクノードはグラフを充足するためにそれら自身を表示すると解釈されなければならないので,グラフのスコレム化のエルブラン解釈はブランクノード写像と一緒のグラフのエルブラン解釈と同型である.すなわち,Herb(sk(G))
= Herb(G)+B (表記法のよく知られた乱用により,エルブラン解釈におけるブランクノードをスコレム名と同様に扱う)
内挿のレンマ. もし S
のサブグラフが E のインスタンスならば,そしてそのときのみ,S は E を伴意する..
証明. 'もし' はサブグラフとインスタンスレンマから導かれる.
'そのときのみ' はエルブラン構成を使う.S は E を単純に伴意するとしよう. するとHerb(S)
は S を充足する. 故に,Herb(S)
は E を充足する. すなわち,E のブランクノードから IRHerb(S) への写像に対して, [Herb(S)+A]
は E 中のすべての
s p o .
を充足する.したがって,S はトリプル
[Herb(E)+A](s)
p [Herb(E)+A](o)
.
を含まなければならない.
それはインスタンス写像 A
の下での以前のトリプルのインスタンスである.それゆえ,そのような すべてのトリプル集合は E のインスタンスである S のサブグラフとなる.
QED
次は内挿レンマの直接的な帰結である.
匿名性のレンマ. E を簡約なグラフとし, E' を E の真のインスタンスとする.そのとき E は E' を伴意しない.
証明. 仮に E が E' を伴意するとしよう.すると E のサブグラフは E' のインスタンスであり,
それゆえ,E の真のインスタンスとなる.したがって,E は 簡約ではない.これは仮説に矛盾する.
したがって E は E' を伴意しない.
QED
コンパクト性レンマ. もし
S が E を伴意し,E が有限のグラフならば,S の有限な部分集合で E を伴意するものがある.
証明. 内挿レンマによって,S のサブグラフ S' は E のインスタンスである. よって,S'
は有限である.そして S' は E を伴意する.
QED
コンパクト性は単純伴意ではあたりまえであるけれども,もっと精巧な意味論的拡張ではそんなにあたりまえなものにはならない.
単調性レンマ. S を S' のサブグラフとし,S は E
を伴意するとしよう.すると S' は E を伴意する. (一般的単調性レンマの特殊な場合)
QED
一般的単調性レンマ. S と S' を,S のすべてのメンバーが
S' のどれかのメンバーのサブセットであるような s の集合としよう. Y は X の意味論的拡張を指示するとして,S が E を X-伴意するとして,S と
E は Y の構文論的制限を満たすものとする.そのとき,S' は E を Y-伴意する.
証明.これは単純に定義を追跡すれば得られる. I を S の Y-解釈としよう.そのとき,Y は X
の意味論的拡張なので, サブグラフとマージのレンマによって,I は S を充足し,故に I は E
を充足する.
QED
以下の二つの証明は,内挿レンマの証明に用いられた一般化の共通のパターンに従って,ルールを余すところ無く適用して得られる '閉包'
に作用するエルブラン構成の修正を用いる.その証明は,結果の解釈が語彙にも適切であるし エルブラン解釈にも同様に作用することを示すことによって,証明されなければならない.証明の複雑さは多分に,リテラル値を正しく考慮するために,エルブラン構成を改造しなければならないということから生ずる.エルブラン解釈はリテラルの型を無視して,すべての型付きリテラルを非リテラル値であるかのように扱う.これは型付きリテラルを単に名前の表示のように扱う単純伴意を考慮するときには重要ではないけれども,
rdf- そして rdfs-解釈を考慮するときにはもっと注意深さが必要となる.
どちらの証明においても,扱いにくい表記法が必要ではあるが,基本的に素直に理解される一つの基本的なアイデアが用いられる.単純エルブラン解釈はすべての語彙アイテムをそれら自身であるかのように扱って,これらの構文論的アイテムからその解釈を構築するが,rdf-
および
rdfs-解釈についての意味論的条件は,特にXMLリテラルが他の種類のエンティティを表示するのに必要なすべての場合にこれを許さない.それゆえ,我々は,できるかぎり同定写像に近いけれども,これら特別なリテラル値に適用されるときにはグラフ中のその値の証拠として働く特定のブランクノードを同定する写像,解釈のユニバースからグラフの語彙(加えてブランクノード)への写像
sur を定義することにより 'ほんとうの' 意味論的条件とその構文的 '代用物' を区別することとした. RDFS
の場合には,代理の写像はすべてのリテラル値に拡張される.リテラルにアロケイトされるブランクノードは,サブジェクトの位置で起きることがあるので,そのリテラル値についてのレコード情報は,解釈時のその値に戻されなければならない.
RDF 伴意レンマ. もしルール
lg と RDF
伴意ルール の適応によって, S に加えてRDF
公理トリプルから導かれるグラフがあって,それが E を単純伴意するのなら,そしてそのときのみ, S は E を rdf-伴意する.
証明.'もし' を示すためには,そのルールが rdf-正当であることを言えばよい.
これは読者の演習として残してある.もし S あるいは E が空であれば,そのときの結果は当然である.したがって, 両方とも空ではないと仮定せよ.
'そのときのみ' を証明するには,証明は 単純エルブラン解釈が単純解釈のために行う rdf-解釈に対する役割と同様な役割を果たす,S のrdf
エルブラン解釈 RH を構成することで進められる.その解釈はできるかぎりエルブラン構成に従うが, RDF
意味論条件が充足されるように,well-formed なXMLリテラルを解釈する.その結果, RDF 閉包, C
中のトリプルにガイドされて,次のプロセスから得られるグラフが定義される.
すべてのRDF
公理トリプルを S に加える
ルールによってグラフが変化しなくなるまで,well-typed なXMLリテラルを含むどんなトリプルにも ルール
lg を適応する
グラフが変化しなくなるまで,ルールrdf2
を適応する
グラフが変化しなくなるまで,ルールrdf1
を適応する
C はルール
lg によって,S 中の各リテラルに アロケイトされた正確に1個の新しいブランクノード
_:nnn を含む ことに注意されたい.well-typed なXMLリテラルを含む S
中のトリプルのサブグラフは,そのリテラルがブランクノードに置き換えられて 正確に C 中に再生産され,ルールrdf2
によって導入される トリプル
_:nnn rdf:type rdf:XMLLiteral
.
が追加される.その証明はルール
lg が well-typed な
XMLリテラルに用いられることだけを要求し,その結果実際に少しだけきっちりとした結果となるということにも注意されたい.
ルール
lgによって導入されるブランクノードは トリプルのサブジェクト位置における well-formed なXMLリテラルの代用物
である. (次のレンマの証明ではこれがすべてのリテラルに展開される.) RDF
解釈を構成するために,XMLリテラルとその代用物は解釈の領域における適切なリテラル値に置き換わられなければならないが,
その証明においては,各XMLリテラル値はそれが表示する字句上のアイテムに,ユニークに関係づけられなければならない.
これは次の構成において,細かな気遣いをいくらか必要とする.
もし lll が well-formed なXMLリテラルならば,xml (lll) を lll の XML値とする. そして,C
中の well-formed なXMLリテラルの各XML値に対して,sur (x) を ルール
lgによりそのXMLリテラルにアロケイトされたブランクノードとし, sur を C 中の
URI参照,ブランクノード,その他のリテラルに拡張する.
すると RH は以下で定義される.
|
LVRH = C および {xml (x): x は well-typed な S
中のXMLリテラル} におけるすべてのプレーンリテラル
IRRH = LVRH および C 中にある
URI参照,ブランクノード,その他の型付きリテラルの集合
IPRH = { x:C はトリプル x rdf:type rdf:Property .
を含む.}
もし x が IPRH の元ならば,IEXTRH(x) = {<s,o>:C
はトリプル sur(s) x sur(o) . を含む.}
ISRH は S 中の URI参照 上への同定写像
もし x が S 中の well-formed なXMLリテラルならば,ILRH(x) =
xml(x), さもなければ ILRH(x) = x |
C 中のブランクノード上への写像 B を次のように定義する. もし x が well-formed なXMLリテラル lll
にアロケイトされるのなら,B(x)=xml(lll), さもなければ,B(x)=x.そのときあきらかに [RH+B] は C したがって
S を充足し,故に RH は S を充足する.
C はすべての必要な RDF 公理トリプルを含むので,RH はそれらを充足する.
すべての well-typed なXMLリテラル lll に対して,ルールrdf2
は,IEXTRH(rdf:type) が <xml
(lll),rdf:XMLLiteral> を含むことを要求し,それによって導入されたトリプルに対して,最初の二つの RDF
意味論的条件が充足されることは容易に分かる.
3番目の
RDF 意味論的条件は, 構成によって単純には充足されない,ネガティブな意味論的条件にすぎないが,それが充足することは自明である.
ill-typed なXMLリテラルは RH 中ではそれ自体を表示し,それゆえ構成すると LVRH からは排除される.
リテラルはサブジェクトの位置に来ることはないので,ペア <lll, rdf:XMLLiteral> が
IEXTRH(rdf:type) に現れることはない.したがってその条件は充足され,故に RH は
rdf-解釈となる.
S は E を rdf-解釈するので,RH は E を充足する.故に,E のブランクノードから IRRH へのある写像 A
において, [RH+A] は E 中のすべてのトリプル
s p o
.
を充足する.すなわち,IEXTRH(p) は
<[RH+A](s),[RH+A](o)> を含む.すなわち,C はトリプル
sur([RH+A](s)) p
sur([RH+A](o)).
を含む.しかしこれはインスタンシエーション写像 x ->
sur(A(x)) の下での最初のトリプルのインスタンスであり, 故に C のサブグラフは E のインスタンスとなり,故に C は E
を単純に伴意する.
QED
このレンマはいかなるグラフも充足するrdf-解釈を有していることを示し,その証明は well-formed
なXMLリテラルを適切に解釈して,外延のないプロパティの存在を可能にすることで閉包のエルブラン解釈からどのようにそれを構成したらよいかという方法を説明する.もし
E が有限であれば,導出された C のサブグラフもまた有限であることを注意しておく.
RDFS 伴意レンマの証明は,構造的に類似であり,非常に類似の定義を用いるけれども, rdfs:Literal と
rdfs:Resource
のクラス外延がすべてのリテラル値を含むことを確実にするためにもちろんもっと長くて,より手の込んだ構成が必要である.
RDFS
伴意レンマ. ルール
lg, ルール
gl そして RDF
および RDFS
伴意ルールを適応することで, S に加えてRDF
および RDFS
公理トリプルから得られるグラフがあって,それが単純に E を伴意するかあるいは XMLクラッシュならば,そしてそのときにのみ, S は E をrdfs-伴意する.
証明.'もし' を示すには,再び,RDFS
伴意ルールが rdfs-正当であることを示せばよい.それは再び演習としてとってある.空の場合はあきらかである.
'そのときのみ' の証明は前のレンマに用いられたものと類似で,RDFS 閉包 D が以下に示すプロセスから得られるグラフと
定義されること以外は,似た構造と述語が用いられる
すべての RDF
と RDFS
公理トリプルを S に追加する.
グラフが変化しなくなるまで,リテラルを含むすべてのトリプルに ルール
lg を適応する.
グラフが変化しなくなるまで,ルール rdf2
と rdfs1
を適応する.
グラフが変化しなくなるまで,ルール rdf1,
ルール
gl と残りの RDFS
伴意ルール を適応する.
前のレンマとは異なり,この証明は,すべてのリテラルにルール
lgを,たとえそれが ill-typed なXMLリテラルであっても, 適応することを要求し,逆のルール
glの適応を要求する. ルール
gl は,ルール rdfs6
や rdfs10
だけがサブジェクトのブランクノードをオブジェクト位置に移すので, これらのルールを適応したあとでしか,用いられない.D はルール
lgにより,S 中の各リテラルにつき正確に1個の新しいブランクノード _:nnn を含むことに 注意されたい.リテラルを含む S
中のトリプルのサブグラフは,リテラルに置き換えられたこのブランクノードと,ルールrdfs1によって導入される付加的なトリプル
_:nnn rdf:type rdfs:Literal .
と,ルールrdf2
によって適時多分に導入されるトリプル
_:nnn rdf:type rdf:XMLLiteral
.
を有する D
中に正確に再生産される.リテラルを含むトリプルに引き続き適応されるいずれのルールも,ブランクノードにアロケイトされて置き換えられた
リテラルのある類似のトリプルにも同様に適応されるので,これは構成中のこの時点以降,リテラルは実効的に無視されるということを意味している.
残りの証明においては,これが該当のリテラルにアロケイトされたブランクノードに重ねあわされる意味論的条件をまさしく満たす解釈において
リテラル値を必要であるとして,リテラルを含むグラフのトリプルを無視することに用いられる. ルール
glを使うことで,D が,もしアロケイトされたブランクノードで置き換えられた
リテラルを有する類似トリプルを含むとき,そしてそのときのみに,トリプルがリテラルを含むようにすることができる.
前の証明と同様に,もし lll が well-formed なXMLリテラルならば,xml (lll) は lll
のXML値だとしよう.そのとき, 代理の写像sur は次のように拡張される.最初に,sur の領域は,URI参照,D
中にあるリテラルとブランクノード, そして D 中の well-formed
なXMLリテラルのすべてのXML値を含む集合である.(これは以下に定義される,rdfs-エルブラン解釈のユニバースである.) さて,もし lll が D
中の well-formed なXMLリテラルならば,sur (xml (lll)) をルール
lgによって lll にアロケイトされたブランクノードとし, その他の D 中のリテラル lll に対してはsur(lll)
をルール
lg によって lll にアロケイトされたブランクノードとし そしてすべてのURI参照と D
中のブランクノードに対しては,sur(x) = x とする. sur の値域はURI参照と D
中のブランクノードであることに注意されたい.
そのとき,S の rdfs-エルブラン解釈 SH は,前のレンマと同じように構成される.
|
LVSH = {x: D はトリプル sur(x) rdf:type
rdfs:Literal . を含む.}
IRSH = LVSH に加えて set of URI 参照,D 中のブランクノードおよび
well-formed なXMLリテラル以外のリテラル
IPSH = { x: D はトリプル sur(x)
rdf:type rdf:Property . を含む.}
もし x が IPRH 中の元ならば,IEXTRH(x) = { <s,o>: D
はトリプル sur(s) x sur(o) . を含む.}
ISSH は S 中のURI参照に関する同定写像
もし x が S 中の well-formed なXMLリテラルならば ILSH(x) =
xml(x), さもなければ ILSH(x) = x |
B(x) を以下のように定義する.もし x が D 中の well-formed なXMLリテラル lll
にアロケイトされたブランクノードなら,B(x) = xml (lll). もしそれが D
中の他のリテラルにアロケイトされるのなら,B(x)=lll さもなければ B(x)=x. そのとき,あきらかに [SH+B] は D 故に S
を充足し,故に SH は S を充足する.
前のレンマと同様に,SH は必要なすべての RDF と RDFS 公理トリプルを充足し,構成による最初の二つの RDF 意味論条件を充足する.
SH は D がXMLクラッシュを含まない場合に,三番目の RDF 意味論条件を充足する.ill-typed なXMLリテラルに対する代理の存在は,
前のレンマで用いられた議論では正しくないが,この条件ではあたりまえに充足される.故に,D はXMLクラッシュを含まないと仮定する.
本文で述べたように,我々は最初の RDFS 意味論条件を ICEXT と IC を定義するものとみなすことができる.
したがって,これ以上コメントしたり IEXT に関してすべての条件を記述したりはしない.SH が残りの RDFS 意味論的条件を充足することを示すために,
エルブラン解釈の最小性(minimality)と閉包の完全性を用いて,ケースごとに議論する.
これら諸条件はすべて,ルールを該当の順番に適応することでありのままに反映される.議論の一般的な形式は 2番目の
RDFS 意味論的条件の場合において説明される. <x,y> は
IEXTSH(rdfs:domain) の元,<u,v> は
IEXTSH(x) の元とする. そのとき,D はトリプル
sur(x) rdfs:domain sur(y)
.
sur(u) x sur(v).
を含まなければならず,それゆえ x は URI参照 でなければならず,それゆえ sur(x)=x である.そのとき,ルールrdfs2
によって,それはトリプル
sur(u) rdf:type sur(y).
も含まなければならない.故に IEXTSH(rdf:type) は <u,v>
を含み,故にその条件は満たされる.
その他の場合は,ルールと公理トリプルを用いて意味論的条件の派生物に翻訳することで,同様に進められる.議論の形式は次の表にまとめられる.
いくつかの意味論的条件は数個の下位条件に分割され,いくつかは場合わけされる.
| RDFS 意味論的条件 |
派生物 |
もし x が IR の元ならば
<x,rdfs:Resource> は
IEXT(rdf:type) の元 |
サブジェクトがURI参照かブランクノード:
x a b
x rdf:type rdfs:Resource |
rdfs4a |
リテラル:
_:x rdf:type rdfs:Literal
rdfs:type rdfs:range
rdfs:Class
rdfs:Literal rdf:type rdfs:Class
rdfs:Literal
rdfs:subClassOf rdfs:Resource
_:x rdf:type rdfs:Resource |
以下参照
axiomatic
rdfs3
rdfs8
rdfs9 |
オブジェクトがURI参照かブランクノード:
a b x
x rdf:type rdfs:Resource |
rdfs4b |
|
プレディケイトがURI参照」:
a x b
x rdf:type rdf:Property
rdf:type
rdfs:domain rdfs:Resource
x rdf:type rdfs:Resource |
rdf1
axiomatic
rdfs2 |
x は LV の元,もし
<x,rdfs:Literal> が IEXT(rdf:type)
の元ならば,そしてそのときのみ |
well-typed なXMLリテラル lll:
a b lll
_:x rdf:type
rdf:XMLLiteral
rdf:XMLLiteral rdfs:subClassOf rdfs:Literal
_:x
rdf:type rdfs:Literal |
lg,
rdf2,
sur(xml(lll))=_:x
axiomatic
rdfs9 |
|
それ以外のリテラル lll :
a b lll
_:x rdf:type rdfs:Literal |
lg,
rdfs1,
sur(lll)=_:x |
もし
<x,y> が IEXT(rdfs:domain) の元,かつ <u,v> は IEXT(x)
の元
ならば
<u,y> は IEXT(rdf:type) の元 |
x rdfs:domain y .
u x v .
u rdf:type y . |
rdfs2 |
もし
<x,y> が IEXT(rdfs:range) の元,かつ <u,v> は IEXT(x) の元
ならば
<v,y> は IEXT(rdf:type) の元 |
x rdfs:range y .
u x v .
v rdf:type y . |
rdfs3 |
|
もし
<x,rdf:Property> が IEXT(rdf:type)
の元
ならば
<x,x> は IEXT(rdfs:subPropertyOf) の元 |
x rdf:type rdf:Property
x rdfs:subPropertyOf x |
rdfs6 |
もし
<x,rdf:Property> が IEXT(rdf:type)
の元
<y,rdf:Property> が IEXT(rdf:type)
の元
<z,rdf:Property> が IEXT(rdf:type) の元
<x,y> が
IEXT(rdfs:subPropertyOf) の元
<y,z> が IEXT(rdfs:subPropertyOf)
の元
ならば
<x,z> は IEXT(rdfs:subPropertyOf) の元 |
x rdfs:subPropertyOf y
y rdfs:subPropertyOf z
x subPropertyOf
z |
rdfs5 |
|
もし
<x,y> が IEXT(rdfs:subPropertyOf) の元
<u,v> が
IEXT(x) の元
ならば
<x,rdf:Property> は IEXT(rdf:type)
の元
<y,rdf:Property> は IEXT(rdf:type) の元
<u,v> は
IEXT(y) の元 |
x rdfs:subPropertyOf y
u x v
rdfs:subPropertyOf rdfs:domain
rdf:Property
x type rdf:Property
rdfs:subPropertyOf rdfs:domain
rdf:Property
y rdf:type rdf:Property
u y v |
axiomatic triple
rdfs2
axiomatic
triple
rdfs3
rdfs7 |
もし
<x,rdfs:Class> が IEXT(rdf:type) の元
ならば
<x,rdfs:Resource> は IEXT(rdfs:subClassOf) の元 |
x rdf:type rdfs:Class
x rdfs:subClassOf rdfs:Resource |
rdfs8 |
|
もし
<x,y> が IEXT(rdfs:subClassOf) の元
<u,x> が
IEXT(rdf:type) の元
ならば
<x,rdfs:Class> は IEXT(rdf:type)
の元
<y,rdfs:Class> は IEXT(rdf:type) の元
<u,y> は
IEXT(rdf:type) の元 |
x rdfs:subClassOf y
u rdf:type x
rdfs:subClassOf rdfs:domain
rdfs:Class
x rdf:type rdfs:Class
rdfs:subClassOf rdfs:range
rdfs:Class
y rdf:type rdfs:Class
u rdf:type y |
axiomatic triple
rdfs2
axiomatic
triple
rdfs3
rdfs9 |
もし
<x,rdfs:Class> が IEXT(rdf:type)
の元
ならば
<x,x> は IEXT(rdfs:subClassOf) の元 |
x rdf:type rdfs:Class
x rdfs:subClassOf x |
rdfs10 |
もし
<x,rdfs:Class> が IEXT(rdf:type)
の元
<y,rdfs:Class> が IEXT(rdf:type) の元
<z,rdfs:Class> が
IEXT(rdf:type) の元
<x,y> が IEXT(rdfs:subClassOf)
の元
<y,z> が IEXT(rdfs:subClassOf) の元
ならば
<x,z> は
IEXT(rdfs:subClassOf) の元 |
x rdfs:subClassOf y
y rdfs:subClassOf z
x rdfs:subClassOf z |
rdfs11 |
もし
<x,rdfs:ContainerMembershipProperty> が IEXT(rdf:type)
の元
ならば
<x,rdfs:member> は IEXT(rdfs:subPropertyOf) の元 |
x rdf:type rdfs:ContainerMembershipProperty
x rdfs:subPropertyOf
rdfs:member |
rdfs12 |
もし
<x,rdfs:Datatype> が IEXT(rdf:type)
の元
ならば
<x,rdfs:Literal> は IEXT(rdfs:subClassOf) の元 |
x rdf:type rdfs:Datatype
x rdfs:subClassOf rdfs:Literal |
rdfs13 |
それゆえ SH は rdfs-解釈である.
S は E を rdfs-伴意するので,SH は E を充足する.ゆえに E のブランクノードから IRSH へのある写像 A
に対して, [SH+A] は E 中のすべてのトリプル
s p o
.
を充足する.すなわち,IEXTSH(p) は
<[SH+A](s),[SH+A](o)> を含み,すなわち,D はトリプル
sur([SH+A](s)) p sur([SH+A](o)).
を含む.これは,もし o がリテラルでなければ,インスタンシエーション写像 x -> sur(A(x))
の下で最初のトリプルのインスタンスである. もし o がリテラルなら,sur([SH+A](o) は o
にアロケイトされたブランクノードであり,ゆえに D は次のトリプルを含む.
sur([SH+A](s)) p o .
これはインスタンシエーション写像 x -> sur(A(x)) の下での最初のトリプルのインスタンスである.ゆえに D
のサブグラフは インスタンシエーション写像 x -> sur(A(x)) の下で E のインスタンスであり,ゆえに D は E
を単純伴意する.
ゆえに D はXMLクラッシュを含むかあるいは E を単純伴意する.ゆえに D はレンマの条件を充足する.
QED
もし E が有限であれば,あるいは D がXMLクラッシュを含むなら,D の有限サブグラフもまたレンマの条件を充足することに注意されたい.
付録 B: 述語用語集 (情報提供)
前件(Antecedent) (n.) 推論において,それから
結論が引き出されるところの表現.
伴意関係においては,伴意するもの(entailer).
仮説でもある.
表明(Assertion)
(n.) (i) 真であることを主張する任意の表現.(ii) 何かを真であると主張する行為.
クラス(Class) (n.)
一般的概念,カテゴリあるいは分類.主に事物の分類やカテゴリ化に用いられるもの.RDFにおいては,形式的に,型 rdfs:Class
のリソースであり,rdf:type
property の値としてそのクラスを持つすべてのリソースの集合と関連する.クラスは形式論理の文献ではしばしば
'述語(predicate)' と呼ばれる.
(class とset はしばしば同一とされるが,RDF では両者を区別する.クラスを集合と区別することで 前述したように,RDF
ではより自由にクラス階層を構成することができる.)
完全である (adj.,
推論システムについて). (1) 二つの任意の表現の間ですべての伴意が検出できること.
(2) すべての正当な推論を導くことができること.
推論
を参照のこと.限量子とともにも用いられて,ある限られた形式あるいは本質(例えばある正規形式におけるあるいはある構文的条件に合致した表現)
において伴意を検出あるいはすべての正当な推論を導くことができること.
(この二つの定義は,最初の定義ではシステムは伴意の帰結にアクセスする必要があるけれども,(p and p) から p を導くといった 'あたりまえの'
推論を導くことができないので,正確には等しくない.典型的には,実効的な推論システムは一番目の意味では完全かもしれないが,二番目の意味ではかならずしもそうではない.)
帰結(Consequent) (n.) 推論において,前件部から構成された表現.伴意関係においては,伴意される側(entailee).結論
ともいう.
矛盾しない(Consistent) (adj., 表現について) 充足する解釈があって,内部で矛盾しないこと
(推論システムでは正しい の同義語としても用いられる.)
正しい (adj.,
推論システムについて) いかなる正しくない推論も引き出せないこと,あるいは間違った伴意の主張を作れないこと.推論 を見よ.
決定可能(Decideable) (adj., 推論システムについて)
有限の時間と有限の資源で,どんな表現のペアについても,一番目が二番目を伴意するかどうか決定できること. (同じく: adj., 論理について)
その論理の意味論に対して完全かつ正しい,決定可能な推論システムがあること.
(すべての論理に完全かつ決定可能な推論システムがあるわけではなく,決定可能な推論システムは任意の計算複雑性をもつ可能性がある.論理の構文論,意味論と推論システムの複雑性との関係は,無視できない研究内容であり続けている.)
伴意する (v.),
伴意 (n.)
一番目が真がいつでもその二番目も真であることを保障するような表現間の意味論的関係.等価であるが,一番目の表現が真で二番目が偽となることが論理的にいかなるときも不可能であること.等価であるが,一番目を充足する
いかなる解釈も,二番目を充足すること.
(表現のある集合とある表現の間でも用いられる.)
等価な(Equivalent) (prep., to と一緒に)
表明されたとき,世界に関する同一の主張を作って,正確に同じ条件下で真であること, 伴意してかつ伴意される.
外延的(Extensional) (adj., of a logic)
集合論に基づく理論あるいはクラス理論.クラスは集合と考えられ,プロパティは <object, value>
ペアの集合と考えられる.同じ外延を有するエンティティ間で違いを認めない理論.内包的を参照.
形式的(Formal) (adj.)
通常の数学的テクニックを用いて,確立された結果を可能にするように十分に正確に言い表わすこと
もしそしてそのときのみ(Iff) (conj.)
'if and only if' の慣習的な省略.必要十分条件を表すために用いられる.
矛盾する(Inconsistent) (adj.)
すべての解釈において偽, 充足不可能であること.
矛盾(Inconsistency) (n.) 任意の矛盾する表現あるいはグラフ.
(ちょうど (A and not-B) が矛盾するときに A は B を伴意するので,伴意と矛盾には密接な関係がある.
伴意の第2定義を参照せよ.これは多くの機械的推論システムの基礎である.
無矛盾(consistency)と矛盾の定義は厳密に双対であるけれども,計算的には似ていない.すべての場合に矛盾を検出することよりもすべての場合に無矛盾を検出することのほうがしばしば難しい.)
Indexical
(adj., of an expression) having a meaning which implicitly refers to the context
of use. Examples from English include words like 'here', 'now', 'this'.
推論(Inference)
(n.) 既存の表現から新しい表現を構成する行為またはプロセス,あるいはそのような行為やプロセスの結果.伴意に一致する推論は
正しい(correct) あるいは 正当(valid)
であると言われる.
推論ルール(Inference rule)
推論のタイプの形式的な記述.推論システム(inference system),
組織化された推論ルールのシステム.また,推論するあるいは推論の正当性をチェックするソフトウェア.
内包的(Intensional) (adj., of a logic) 外延的ではない.同じ外延を有する異なるエンティティを許す.
(内包性の利点と欠点は哲学的論理の文献において,広く議論されてきた.外延的意味論は単純で,形式論理のためのこれまでの意味論では外延的見方を仮定してきたが,通常の言語の概念解析では,内包的な考えのほうが自然であることが示唆されている.外延的論理ではすべての
'空' な外延を同じものと取り扱わざるをえない例がしばしば引用される.'丸い四角' を 'サンタクロース'
と同一視しなければならないし,「体毛が無く二足歩行のヒト科の動物」と「人間」のように 'たまたま'
同じインスタンスを持つ異なる概念を区別することができない.)
解釈(Interpretation) (of)
(n.) いかなる論理表現においても真偽を確立するにちょうど十分な世界の諸相の最小の形式的な記述.
(ある種の論理テキストでは,解釈構造,どんな特定の語彙とも独立なものとして考慮される '可能世界'
,とある語彙からその構造への解釈写像 を区別して認識する.RDF
意味論ではこれらを一つの概念に一緒にして,もっと簡単なやりかたを採用する.)
論理(Logic) (n.) 命題を表現する形式的言語.
形而上学の(Metaphysical) (adj.)
何か絶対的なあるいは基礎的な意味において事物の本質についてかかわること
モデル理論(Model
Theory) (n.) 表現を解釈と関係付ける形式的意味論.
( 'モデル理論'
という名前は論理意味論における伝統的な使用法からきている.そこでは充足する解釈が「モデル」と呼ばれていた.しかし,この使用法は「計算モデル」のような用語に含まれる意味とほとんどまったく逆の意味なので,この文書では使用が避けられた.)
単調な(Monotonic)
(形容詞, 論理システムあるいは推論システムの) もし S が E を伴意するのなら (S + T) も E
を伴意するという条件を充足すること,すなわちある前提に情報を追加してもある正当な
伴意を非正当にすることはできないということ.
(通常のモデル理論と伴意の標準的概念に基づくすべての論理は単調である.単調論理は伴意が生成された文脈の外でも
正当のままであるという性質を有する.これが何故
RDF は単調であるべきとされたかの理由である.)
非単調な(Nonmonotonic)(形容詞, 論理システムあるいは推論システムの)
単調ではないこと.非単調の形式論は
AI と様々なアプリケーションにおいて提案され用いられている.非単調推論の例として デフォールト論理
がある.そこではより特別な情報によって矛盾しないかぎり,「典型的な」一般的な真が仮定される.(鳥は普通は飛ぶが,ペンギンは飛ばない);
失敗による否定 ,論理プログラミングシステムで通常仮定される.そこではある命題の証明の失敗からその命題の偽を結論する;
暗黙的閉世界仮説
,データベースアプリケーションにしばしば仮定される.そこでは,あるコーパス中のあるエンティティについての情報の欠落から,その情報を偽と結論する.(例えば,もし誰かが従業員データベース中のリストに無ければ,その人物は従業員ではない.)
(単調推論と非単調推論の関係はしばしば微妙である.例えば,もし閉世界仮説が明示的になされるのなら,例えば,コーパスが完全で帰結において情報源が明示されているのなら,閉世界推論は単調である.盲信が推論を非単調にする.非単調の結論はある種の「文脈」においてのみ,正当であるとしか言えず,その文脈の外で用いられるときには誤りまたは誤解に陥りやすい.推論において文脈を明示的にして,結論中で目に見えるようにすることは単調の枠組みに組みなおす方法である.)
オントロジー上の(Ontological) (adj.) (哲学)
事物のどんな質が本当に存在するのかということにかかわること.(応用で) あるトピックや領域の形式的記述にかかわること.
命題(Proposition) (n.)
真偽値を持つもの.真あるいは偽である宣言や表現.
(言語哲学的分析では,伝統的に,命題を述べるのに用いられる表現と命題を区別してきた.しかしモデル理論ではこの違いは必要ではない.)
具体化する(Reify) (v.),
具体化(reification) (n.)
オブジェクトとしてカテゴリ化すること.エンティティとして記述すること.構文論的表現を意味的なオブジェクトとして扱って,他の構文を用いてそれ自身を記述するのに用いられる約束事の記述にしばしば用いられる.RDF
では,具体化されたトリプルとは別の RDF トリプルを用いた,トリプルトークンの記述である.
リソース (n.)(RDF
に用いられて) (i) エンティティ;ユニバース中のもの.(ii) あるクラス名として: すべてのもののクラス;可能な限り最大に包含する概念.
充足する(Satisfy)
(v.t.), 充足(satisfaction),(n.) 充足する(satisfying)
(adj., 解釈において). 真とすること.解釈と表現の間の基本的な意味関係.X が Y を充足するとは,もし世界が
X によって記述される条件に合致するならば,Y が真とならなければならないということ.
意味論的(Semantic)
(adj.) , 意味論(semantics) (n.)
意味の明細にかかわること.表現とそれが表示するものとの違いを強調するために,構文論 としばしば対比される.
スコレム化
(n.) ブランクノードが '新しい' 名前に置き換えられる構文上の変換
(厳密には正当ではないけれども,スコレム化は表現の基本的な意味を保持して,機械推論システムにおいてしばしば用いられる.その名前は論理学者
A.
T. Skolem にちなんでつけられた.)
トークン(Token) (n.)
文書中の特定の物理的なシンボルあるいは表現のこと.表現の抽象的な文法の形式 タイプ と通常対比される.
ユニバース(Universe)
(n., 論議の領域 とも言う) 万物の分類,あるいは,解釈が存在するとみなすところのすべての事物の集合.RDF/S
では,リソース集合に同一とされる.
用いる(Use) (v.)
言及する(mention) に対比される.何かを表示するあるいは参照する構文の1片を用いること.言語が用いられる正常な方法.
("ある意味で,我々があるものについて何かを言おうと思うときはいつでも,文章中において,もの自体を使うのではなく,その名前や表示を使わなければならない."
- Alfred Tarski)
正当である(Valid) (adj.,
推論あるいは推論プロセスにおける) 伴意に一致すること.すなわち,推論の前件部によって伴意されるところの結論.正しい(correct)
とも言う.
Well-formed
(adj., 表現の) 構文論的に合法であること.
World (n.)
(the と一緒に) (i) 現実世界.(a と一緒に) (ii) 配置され得たかも知れない実際の世界のあり方.(iii)
ある 解釈.
(iv) 可能世界.
( '可能世界'
の形而上学の状態は,非常に論争的である.さいわいなことに,この2番目や3番目の意味の概念を使うために平行するユニバースについて信念を持つ必要はなく.意味論の目的には十分である.)
付録 C: 謝辞
この文書はRDF Core Working
Groupのメンバーの合同の努力,特に, Jeremy Carroll,Dan Connolly,Jan Grant,R. V. Guha,Graham
Klyne,Ora Lassilla,Brian McBride,Sergey Melnick,Jos deRoo,そして Patrick Stickler
によってなされた貢献の結果である.
基礎の公理に違反することなく自己適応を可能にする明示的な外延写像を用いるという基本的アイデアは,Christopher
Menzelによって示唆されたものである.
Peter Patel-Schneider と Herman ter Horst
は初期の草稿のいくつかの主要な問題点を発見し,いくつかの重要な技術的改善を示唆してくれた.
この文書に関する Patrick Hayes の研究は,一部 DARPA 契約 #2507-225-22 の下で行われた.
- [RDF-CONCEPTS]
- Resource
Description Framework (RDF): Concepts and Abstract Syntax, Graham
Klyne and Jeremy J. Carroll, Editors, W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-concepts-20040210/ . Latest version available at
http://www.w3.org/TR/rdf-concepts/ .
- [RDF-SYNTAX]
- RDF/XML
Syntax Specification (Revised), Dave Beckett, Editor, W3C
Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-syntax-grammar-20040210/ . Latest version available
at http://www.w3.org/TR/rdf-syntax-grammar/ .
- [RDF-TESTS]
- RDF
Test Cases, Jan Grant and Dave Beckett, Editors, W3C
Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-testcases-20040210/ . Latest version available at
http://www.w3.org/TR/rdf-testcases/ .
- [RDFMS]
- Resource Description
Framework (RDF) Model and Syntax Specification , O. Lassila and R.
Swick, Editors. World Wide Web Consortium. 22 February 1999. This version is
http://www.w3.org/TR/1999/REC-rdf-syntax-19990222/. The latest version of RDF M&S
is available at http://www.w3.org/TR/REC-rdf-syntax/.
- [RFC 2119]
- RFC 2119 - Key words
for use in RFCs to Indicate Requirement Levels , S. Bradner, IETF.
March 1997. This document is http://www.ietf.org/rfc/rfc2119.txt.
- [RFC 2396]
- RFC 2396 - Uniform
Resource Identifiers (URI): Generic Syntax Berners-Lee,T., Fielding
and Masinter, L., August 1998
- [XSD]
- XML Schema Part 2:
Datatypes, Biron, P. V., Malhotra, A. (Editors) World Wide Web
Consortium Recommendation, 2 May 2001
- [OWL]
- OWL Web
Ontology Language Reference, Mike Dean and Guus Schreiber, Editors,
W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-owl-ref-20040210/ . Latest version available at
http://www.w3.org/TR/owl-ref/ .
- [Conen&Klapsing]
- A
Logical Interpretation of RDF, Conen, W., Klapsing, R..Circulated
to RDF
Interest Group, August 2000.
- [DAML]
- Frank van Harmelen, Peter F. Patel-Schneider, Ian Horrocks (editors), Reference Description of
the DAML+OIL (March 2001) ontology markup language
- [Hayes&Menzel]
- A
Semantics for the Knowledge Interchange Format, Hayes, P., Menzel,
C., Proceedings of 2001 Workshop on the IEEE Standard
Upper Ontology, August 2001.
- [KIF]
- Michael R. Genesereth et. al., Knowledge Interchange
Format, 1998 (draft American National Standard).
- [Marchiori&Saarela]
- Query +
Metadata + Logic = Metalog, Marchiori, M., Saarela, J. 1998.
- [LBASE]
- Lbase:
Semantics for Languages of the Semantic Web, Guha, R. V., Hayes,
P., W3C Note, 10 October 2003.
- [McGuinness&al]
- DAML+OIL:An
Ontology Language for the Semantic Web, McGuinness, D. L., Fikes,
R., Hendler J. and Stein, L.A., IEEE Intelligent Systems, Vol. 17, No. 5,
September/October 2002.
- [RDF-PRIMER]
- RDF
Primer, Frank Manola and Eric Miller, Editors, W3C Recommendation,
10 February 2004, http://www.w3.org/TR/2004/REC-rdf-primer-20040210/ . Latest version available at
http://www.w3.org/TR/rdf-primer/ .
- [RDF-VOCABULARY]
- RDF
Vocabulary Description Language 1.0: RDF Schema, Dan Brickley and
R. V. Guha, Editors, W3C Recommendation, 10 February 2004,
http://www.w3.org/TR/2004/REC-rdf-schema-20040210/ . Latest version available at
http://www.w3.org/TR/rdf-schema/ .
付録 D:
変化ログ.(情報提供)
15 December
2003 Proposed Recommendation以降の変化.
付録 A における RDFS 伴意ルールの言葉使いにおける誤りが訂正された.用語集と主文におけるいくつかのミスタイプが訂正された.
ter
Horst によるコメントを考慮した結果, D-解釈の定義がデータタイプ名を含む拡張語彙に適応するように修正された.
変化ログの古い項目は削除された.それらは以前の版にある.



